2-opt

In optimization, 2-opt is a simple local search algorithm for solving the traveling salesman problem. The 2-opt algorithm was first proposed by Croes in 1958,[1] although the basic move had already been suggested by Flood.[2] The main idea behind it is to take a route that crosses over itself and reorder it so that it does not.

 - A   B -             - A - B -
     ×         ==>
 - C   D -             - C - D -
2-opt

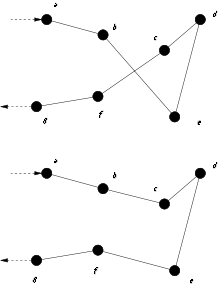
A complete 2-opt local search will compare every possible valid combination of the swapping mechanism. This technique can be applied to the travelling salesman problem as well as many related problems. These include the vehicle routing problem (VRP) as well as the capacitated VRP, which require minor modification of the algorithm.

This is the mechanism by which the 2-opt swap manipulates a given route:

procedure 2optSwap(route, i, k) {
    1. take route[0] to route[i-1] and add them in order to new_route
    2. take route[i] to route[k] and add them in reverse order to new_route
    3. take route[k+1] to end and add them in order to new_route
    return new_route;
}

Here is an example of the above with arbitrary input:

  • Example route: A → B → C → D → E → F → G → H → A
  • Example parameters: i = 4, k = 7 (starting index 1)
  • Contents of new_route by step:
    1. (A → B → C)
    2. A → B → C → (G → F → E → D)
    3. A → B → C → G → F → E → D → (H → A)

This is the complete 2-opt swap making use of the above mechanism:

repeat until no improvement is made {
    start_again:
    best_distance = calculateTotalDistance(existing_route)
    for (i = 1; i <= number of nodes eligible to be swapped - 1; i++) {
        for (k = i + 1; k <= number of nodes eligible to be swapped; k++) {
            new_route = 2optSwap(existing_route, i, k)
            new_distance = calculateTotalDistance(new_route)
            if (new_distance < best_distance) {
                existing_route = new_route
                best_distance = new_distance
                goto start_again
            }
        }
    }
}

Note: If you start/end at a particular node or depot, then you must remove this from the search as an eligible candidate for swapping, as reversing the order will cause an invalid path.

For example, with depot at A:

   A → B → C → D → A

Swapping using node[0] and node[2] would yield

   C → B → A → D → A

which is not valid (does not leave from A, the depot).

See also

References
  1. G. A. Croes, A method for solving traveling salesman problems. Operations Res. 6 (1958) , pp., 791-812.
  2. M. M. Flood, The traveling-salesman problem. Operations Res. 4 (1956) , pp., 61-75.
  • G. A. CROES (1958). A method for solving traveling salesman problems. Operations Res. 6 (1958) , pp., 791-812.
  • M. M. FLOOD (1956). The traveling-salesman problem. Operations Res. 4 (1956) , pp., 61-75.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.