Adiabatic electron transfer

Adiabatic electron-transfer is the basis of oxidation-reduction processes, which are ubiquitous in nature in both the inorganic and biological spheres. The mechanism of these reactions—the simplest of which proceed without making or breaking chemical bonds—remained unknown until the mid 1950s, when several independent theoretical studies showed that it was due to modulation of coupling between electronic and vibrational motions. According to his Royal Society election citation,[1] Noel Hush's research in the area of homogeneous and heterogeneous electron transfer[2] showed that electron transfer occurring during a collision between a molecule and either another molecule or else an electrode surface occurs adiabatically on a continuous potential-energy surface, and that electron transfer can occur by either optical or thermal mechanisms with the corresponding rates being closely connected.[3]

Fig. 1. Electron transfer occurs between donor (D) and acceptor (A) species separated by distance R that may be found in many forms in both condensed phases and the gas phase. Internal structure, external structure, or chance collisions provide interconnection between the species. Upon electron transfer, the structure of the local chemical environments involving D and A change, as does the polarization these species induce on any surrounding media.

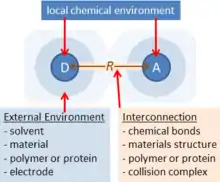
Figure 1 sketches the basic elements of adiabatic electron-transfer theory. Two chemical species (ions, molecules, polymers, protein cofactors, etc.) labelled D (for “donor”) and A (for “acceptor”) become a distance R apart, either through collisions, covalent bonding, location in a material, protein or polymer structure, etc. These species have different chemical bonding environments and they polarize any surrounding condensed media. A key feature is that both species must be able to sustain different charge (valence) states. Electron-transfer theories specify equations describing the rate of charge transfer processes that utilize these different charged states. All electrochemical reactions occur by this mechanism. Adiabatic electron-transfer theory stresses that intricately coupled to such charge transfer is the ability of any D-A system to absorb or emit light. Hence fundamental understanding of any electrochemical process demands simultaneous understanding of the optical processes that the system can undergo.

Fig. 2. When the donor species absorbs light energy, it goes into a high-energy excited state, generating significant changes to its local chemical environment and the polarization of its external environment. These environments facilitate coupling ${\displaystyle V_{DA}}$ between the donor and acceptor, which drives photochemical charge separation with a rate given by Eqn. (3) in the weak-coupling limit. This rate is also dependent on the energy ${\displaystyle \lambda }$ required to rearrange the atoms to the preferred local geometry and environment polarization of the charge-separated state D⁺-A⁻ and the energy change ${\displaystyle \Delta G_{0}}$ associated with charge separation.

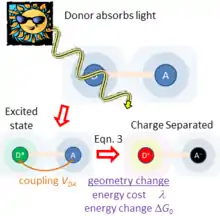
Figure 2 sketches what happens if light is absorbed by just one of the chemical species, taken to be the charge donor. This produces an excited state of the donor. As the donor and acceptor are close to each other and surrounding matter, they experience a coupling ${\displaystyle V_{DA}}$. If the free energy change ${\displaystyle \Delta G_{0}}$ is favorable, this coupling facilitates primary charge separation to produce D⁺-A⁻ , producing charged species. In this way, solar energy is captured and converted to electrical energy. This process is typical of natural photosynthesis as well as modern organic photovoltaic and artificial photosynthesis solar-energy capture devices.[4] The inverse of this process is also used to make organic light-emitting diodes (OLEDs).

Fig. 3. Light energy is absorbed by the donor and acceptor, initiating intervalence charge transfer to directly convert solar energy into electrical energy as D⁺-A⁻. In the weak-coupling limit, the coupling ${\displaystyle V_{DA}}$, reorganization energy ${\displaystyle \lambda }$, and the free energy change ${\displaystyle \Delta G_{0}}$ control the rate of light absorption (and hence charge separation) via Eqn. (1).

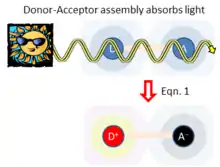
Unifying standard electrochemical electron-transfer processes with this type of solar energy harvesting, adiabatic electron-transfer theory also depicts a third application in which the donor and acceptor are both involved in light absorption, as sketched in Figure 3. Here, light absorption directly leads to charge separation D⁺-A⁻. Hush's theory for this process[3] considers the donor-acceptor coupling ${\displaystyle V_{DA}}$, the energy ${\displaystyle \lambda }$ required to rearrange the atoms from their initial geometry to the preferred local geometry and environment polarization of the charge-separated state, and the energy change ${\displaystyle \Delta G_{0}}$ associated with charge separation. In the weak-coupling limit ( ${\displaystyle 4V_{DA}^{2}/\lambda ^{2}\ll 1}$), Hush showed[3] that the rate of light absorption (and hence charge separation) is given from the Einstein equation by

${\displaystyle k\propto {\frac {V_{DA}^{2}R^{2}}{\lambda +\Delta G_{0}}}.}$ … (1)

This theory explained[3] how the world's first modern synthetic dye, Prussian blue absorbes light, creating[5] [6][7] [8][9] the field of intervalence charge transfer spectroscopy.

Hush's theory also provides theoretical underpinning for the Robin-Day classification system[10] for mixed-valence systems. Mixed valence is widespread in chemistry, from superconductors to minerals, magnetic molecular clusters and enzymes. It occurs when the same chemical species is found in two formally different oxidation states in the same system.[11]

The synthesis of the mixed-valence Creutz-Taube ion, an event leading significantly to the award of the 1983 Nobel Prize in Chemistry to Henry Taube, demonstrated the successfulness of adiabatic electron-transfer theory. In this molecule, the coupling ${\displaystyle V_{DA}}$ is not small, delivering unprecedented chemical phenomena in which charge is not localized on just one chemical species but is shared quantum mechanically between two, presenting classically forbidden half-integral valence states. Hush showed[12] that the critical requirement for this phenomenon is

${\displaystyle {\frac {2|J_{DA}|}{\lambda }}\geq 1.}$ … (2)

Adiabatic electron-transfer theory stems from London's approach to charge-transfer and indeed general chemical reactions[13] applied by Hush using parabolic potential-energy surfaces.[14][15] Hush himself has carried out many theoretical and experimental studies of mixed valence complexes and long range electron transfer in biological systems. Hush's quantum-electronic adiabatic approach to electron transfer was unique; directly connecting with the Quantum Chemistry concepts of Mulliken, it forms the basis of all modern computational approaches to modeling electron transfer.[16][17][18][19] Its essential feature is that electron transfer can never be regarded as an “instantaneous transition”; instead, the electron is partially transferred at all molecular geometries, with the extent of the transfer being a critical quantum descriptor of all thermal, tunneling, and spectroscopic processes. It also leads seamlessly[20] to understanding electron-transfer transition-state spectroscopy pioneered by Zewail.

In adiabatic electron-transfer theory, the ratio ${\displaystyle 2V_{DA}/\lambda }$ is of central importance. In the very strong coupling limit when Eqn. (2) is satisfied, intrinsically quantum molecules like the Crautz-Taube ion result. Most intervalence spectroscopy occurs in the weak-coupling limit described by Eqn. (1), however. In both natural photosynthesis and in artificial solar-energy capture devices, ${\displaystyle 2V{_{D}A}/\lambda }$ is maximized by minimiming ${\displaystyle \lambda }$ through use of large molecules like chlorophylls, pentacenes, and conjugated polymers. The coupling ${\displaystyle V_{DA}}$ can be controlled by controlling the distance R at which charge transfer occurs- the coupling typically decreases exponentially with distance. When electron transfer occurs during collisions of the D and A species, the coupling is typically large and the “adiabatic” limit applies in which rate constants are given by transition state theory.[2] However, in biological applications as well as modern organic conductors and other device materials, R is externally constrained and so the coupling set at low or high values. In these situations, weak-coupling scenarios often become critical.

In the weak-coupling (“non-adiabatic”) limit, the activation energy for electron transfer is given by the expression derived independently by Kubo and Toyozawa[21] and by Hush.[15] Using adiabatic electron-transfer theory,[22] in this limit Levich and Dogonadze then determined the electron-tunneling probability to express the rate constant for thermal reactions as[23]

${\displaystyle k={\frac {2\pi V_{DA}^{2}}{\hbar (4\pi \lambda k_{\beta }T)^{1/2}}}\exp {\frac {-(\Delta G_{0}+\lambda )^{2}}{4\lambda k_{\beta }T}}}$. … (3)

This approach is widely applicable to long-range ground-state intramolecular electron transfer, electron transfer in biology, and electron transfer in conducting materials. It also typically controls the rate of charge separation in the excited-state photochemical application described in Figure 2 and related problems.

Marcus showed[24] that the activation energy in Eqn. (3) reduces to ${\displaystyle \lambda /4}$ in the case of symmetric reactions with ${\displaystyle \Delta G_{0}=0}$. In that work,[24] he also derived what is the standard expression for the solvent contribution to the reorganization energy, making the theory readily applicable to practical problems. Use of this solvation description (instead[2] of the form that Hush originally proposed[15]) in approaches spanning the adiabatic and non-adiabatic limits is often termed “Marcus-Hush Theory”.[17][18][25][26] These and other contributions, including the widespread demonstration of the usefulness of Eqn. (3),[27] led to the award of the 1992 Nobel Prize in Chemistry to Marcus.

Adiabatic electron-transfer theory is often also widely applied in Molecular Electronics. In recent years it has been generalized to arbitrary chemical reactions, providing a single conceptual basis covering many different aspects of chemical research.[28] In particular, this reconnects adiabatic electron-transfer theory with its roots in proton-transfer theory[29] and hydrogen-atom transfer,[14] leading back to London's theory of general chemical reactions.[13] In this approach, most chemical processes can be depicted in terms of the three critical parameters ${\displaystyle V_{DA}}$, ${\displaystyle \lambda }$ and ${\displaystyle \Delta G_{0}}$, with for example the resonance energy that makes benzene and all aromatic compounds unique being nothing other than ${\displaystyle V_{DA}}$.[28]

This approach also leads to a simple explanation in terms of the orbital Rydbergization processes discovered by Mulliken as to why first-row elements like nitrogen have bond angles around the tetrahedral angles while later-row elements have very much larger angles.[30] Adiabatic electron-transfer theory applied in a simple one-dimensional form also provides analytical or numerically exact solutions for chemical processes not involving conical intersections, providing critical testbeds for examining failure of the Born-Oppenheimer approximation that is fundamental to chemical understanding.[31] Similarly, it provides a basis for classifying the usefulness of general chemical reactions for applications as qubits in quantum information processors.[32]

References

1. "Fellows Details". Royal Society. Retrieved 18 September 2015.
2. Hush, N. S. (1961). "Adiabatic theory of outer sphere electron-transfer reactions in solution". Transactions of the Faraday Society. 57: 577. doi:10.1039/TF9615700557.
3. Hush, N. S. (1967). Intervalence-transfer absorption. II. Theoretical considerations and spectroscopic data. Progress in Inorganic Chemistry. 8. pp. 391–444. doi:10.1002/9780470166093.ch7. ISBN 9780470166093.
4. Warman, J. M.; Haas, M. P. d.; Paddon-Row, M. N.; Cotsaris, E.; Hush, N. S.; Oevering, H.; Verhoeven, J. W. (1986). "Light-induced giant dipoles in simple model compounds for photosynthesis". Nature. 320 (6063): 615–616. Bibcode:1986Natur.320..615W. doi:10.1038/320615a0. S2CID 4346663.
5. Nelsen, S. F.; Ismagilov, R. F.; Trieber, D. A. (1997). "Adiabatic Electron Transfer: Comparison of Modified Theory with Experiment" (PDF). Science. 278 (5339): 846–849. Bibcode:1997Sci...278..846N. doi:10.1126/science.278.5339.846. PMID 9346480.
6. German, E. D. (1979). "Intramolecular intervalence charge transfer in bimolecular mixed-valence complexes of metals". Chemical Physics Letters. 64 (2): 295–298. Bibcode:1979CPL....64..295G. doi:10.1016/0009-2614(79)80516-3.
7. Sun, D. L.; Rosokha, S. V.; Lindeman, S. V.; Kochi, J. K. (2003). "Intervalence (Charge-Resonance) Transitions in Organic Mixed-Valence Systems. Through-Space versus Through-Bond Electron Transfer between Bridged Aromatic (Redox) Centers". Journal of the American Chemical Society. 125 (51): 15950–15963. doi:10.1021/ja037867s. PMID 14677987.
8. Nelsen, S. F.; Weaver, M. N.; Luo, Y.; Lockard, J. V.; Zink, J. I. (2006). "Use of the neighboring orbital model for analysis of electronic coupling in Class III intervalence compounds". Chemical Physics. 324 (1): 195–201. Bibcode:2006CP....324..195N. doi:10.1016/j.chemphys.2006.01.023.
9. Rosokha, S. V.; Kochi, J. K. (2008). "Fresh Look at Electron-Transfer Mechanisms via the Donor/Acceptor Bindings in the Critical Encounter Complex". Accounts of Chemical Research. 41 (5): 641–653. doi:10.1021/ar700256a. PMID 18380446.
10. Robin, M. B.; Day, P. (1967). Mixed Valence Chemistry-A Survey and Classification. Advances in Inorganic Chemistry and Radiochemistry. 10. pp. 247–422. doi:10.1016/S0065-2792(08)60179-X. ISBN 9780120236107.
11. Day, P.; Hush, N. S.; Clark, R. J. H. (2008). "Mixed valence: origins and developments". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 366 (1862): 5–14. Bibcode:2008RSPTA.366....5D. doi:10.1098/rsta.2007.2135. PMID 17827130. S2CID 5912503.
12. Hush, N. S. (1975). "Inequivalent XPS [x-ray photoelectron spectroscopy] binding energies in symmetrical delocalized mixed-valence complexes". Chemical Physics. 10 (2–3): 361–366. Bibcode:1975CP.....10..361H. doi:10.1016/0301-0104(75)87049-2.
13. London, F. (1932). "On the theory of non-adiabatic chemical reactions". Quantum Chemistry. World Scientific Series in 20th Century Chemistry. 74. pp. 32–60. doi:10.1142/9789812795762_0003. ISBN 978-981-02-2771-5.
14. Hush, N. S. (1953). "Quantum-mechanical discussion of the gas phase formation of quinonedimethide monomers". Journal of Polymer Science. 11 (4): 289–298. Bibcode:1953JPoSc..11..289H. doi:10.1002/pol.1953.120110401.
15. Hush, N. S. (1958). "Adiabatic rate processes at electrodes". The Journal of Chemical Physics. 28 (5): 962–972. Bibcode:1958JChPh..28..962H. doi:10.1063/1.1744305.
16. Kornyshev, A. A.; Tosi, M.; Ulstrup, J. (1997). Electron and Ion Transfer in Condensed Media. Singapore: World Scientific. ISBN 978-9810229290.
17. Kuznetsov, A.; Ulstrup, J. (1998). Electron Transfer in Chemistry and Biology: An introduction to the theory. Chichester: Wiley. ISBN 978-0-471-96749-1.
18. Devault, D. (1980). "Quantum mechanical tunnelling in biological systems". Quarterly Reviews of Biophysics. 13 (4): 387–564. doi:10.1017/S003358350000175X. PMID 7015406.
19. Cave, R. J.; Newton, M. D. (1996). "Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements". Chemical Physics Letters. 249 (1–2): 15–19. Bibcode:1996CPL...249...15C. doi:10.1016/0009-2614(95)01310-5.
20. Reimers, J. R.; Hush, N. S. (2017). "Relating transition-state spectroscopy to standard chemical spectroscopic processes". Chemical Physics Letters. 683: 467–477. Bibcode:2017CPL...683..467R. doi:10.1016/j.cplett.2017.04.070. hdl:10453/125251.
21. Kubo, R.; Toyozawa, Y. (1955). "Application of the Method of Generating Function to Radiative and Non-Radiative Transitions of a Trapped Electron in a Crystal". Progress of Theoretical Physics. 13 (2): 160–182. Bibcode:1955PThPh..13..160K. doi:10.1143/PTP.13.160.
22. Levich, V. G.; Dogonadze, R. R. (1960). "Adiabatic theory for electron-transfer processes in solution". Proc. Akad. Naukl. SSSR. 133: 591.
23. Levich, V. G.; Dogonadze, R. R. (1959). "Theory of rediationless electron transitions between ions in solution". Proc. Akad. Naukl. SSSR. 29: 9.
24. Marcus, R. A. (1956). "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. 1" (PDF). The Journal of Chemical Physics. 24 (5): 966–978. Bibcode:1956JChPh..24..966M. doi:10.1063/1.1742723.
25. Schmickler, W. Electron transfer and single molecule events (PDF). Paris: Eolss Publishers.
26. Efrima, S.; Bixon, M. (1976). "Vibrational effects in outer-sphere electron-transfer reactions in polar media". Chemical Physics. 13 (4): 447–460. Bibcode:1976CP.....13..447E. doi:10.1016/0301-0104(76)87014-0.
27. Marcus, R. A.; Sutin, N. (1985). "Electron transfers in chemistry and biology". Biochimica et Biophysica Acta (BBA) - Reviews on Bioenergetics. 811 (3): 265–322. doi:10.1016/0304-4173(85)90014-x.
28. Reimers, J. R.; McKemmish, L.; McKenzie, R. H.; Hush, N. S. (2015). "A unified diabatic description for electron transfer reactions, isomerization reactions, proton transfer reactions, and aromaticity". Physical Chemistry Chemical Physics. 17 (38): 24598–24617. Bibcode:2015PCCP...1724598R. doi:10.1039/C5CP02236C. PMID 26193994.
29. Horiuti, J.; Polanyi, M. (2003). "Outlines of a theory of proton transfer". Journal of Molecular Catalysis A: Chemical. 199 (1–2): 185–197. doi:10.1016/s1381-1169(03)00034-7.
30. Reimers, J. R.; McKemmish, L.; McKenzie, R. H.; Hush, N. S. (2015). "Bond angle variations in XH3 [X=N,P,As,Sb,Bi]: the critical role of Rydberg orbitals exposed using a diabatic state model". Physical Chemistry Chemical Physics. 17 (38): 24618–24640. Bibcode:2015PCCP...1724618R. doi:10.1039/C5CP02237A. PMID 26190514.
31. Reimers, J. R.; McKemmish, L.; McKenzie, R. H.; Hush, N. S. (2015). "Non-adiabatic effects in thermochemistry, spectroscopy and kinetics: the general importance of all three Born-Oppenheimer breakdown corrections" (PDF). Physical Chemistry Chemical Physics. 17 (38): 24641–24665. Bibcode:2015PCCP...1724641R. doi:10.1039/C5CP02238J. PMID 26196265.
32. McKemmish, L. K.; McKenzie, R. H.; Hush, N. S.; Reimers, J. R. (2011). "Quantum entanglement between electronic and vibrational degrees of freedom in molecules". The Journal of Chemical Physics. 135 (24): 244110. arXiv:1107.1105. Bibcode:2011JChPh.135x4110M. doi:10.1063/1.3671386. PMID 22225147. S2CID 8968217.