Bathtub curve

The bathtub curve is widely used in reliability engineering and deterioration modeling. It describes a particular form of the hazard function which comprises three parts:

• The first part is a decreasing failure rate, known as early failures.
• The second part is a constant failure rate, known as random failures.
• The third part is an increasing failure rate, known as wear-out failures.

The 'bathtub curve' hazard function (blue, upper solid line) is a combination of a decreasing hazard of early failure (red dotted line) and an increasing hazard of wear-out failure (yellow dotted line), plus some constant hazard of random failure (green, lower solid line).

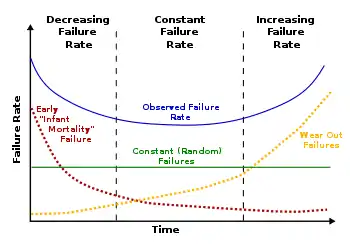
The name is derived from the cross-sectional shape of a bathtub: steep sides and a flat bottom.

The bathtub curve is generated by mapping the rate of early "infant mortality" failures when first introduced, the rate of random failures with constant failure rate during its "useful life", and finally the rate of "wear out" failures as the product exceeds its design lifetime.

In less technical terms, in the early life of a product adhering to the bathtub curve, the failure rate is high but rapidly decreasing as defective products are identified and discarded, and early sources of potential failure such as handling and installation error are surmounted. In the mid-life of a product—generally speaking for consumer products—the failure rate is low and constant. In the late life of the product, the failure rate increases, as age and wear take their toll on the product. Many electronic consumer product life cycles strongly exhibit the bathtub curve.[1]

While the bathtub curve is useful, not every product or system follows a bathtub curve hazard function; for example, if units are retired or have decreased use during or before the onset of the wear-out period, they will show fewer failures per unit calendar time (not per unit use time) than the bathtub curve.

In reliability engineering, the cumulative distribution function corresponding to a bathtub curve may be analysed using a Weibull chart.[1]

See also

• Gompertz–Makeham law of mortality

References

1. J. Lienig, H. Bruemmer (2017). Fundamentals of Electronic Systems Design. Springer International Publishing. p. 54. doi:10.1007/978-3-319-55840-0. ISBN 978-3-319-55839-4.

Further reading

• Klutke, G.; Kiessler, P.C.; Wortman, M. A. (March 2003). "A critical look at the bathtub curve". IEEE Transactions on Reliability. 52 (1): 125–129. doi:10.1109/TR.2002.804492. ISSN 0018-9529.