Brahmi numerals

The Brahmi numerals are a numeral system attested from the 3rd century BCE (somewhat later in the case of most of the tens). They are the direct graphic ancestors of the modern Indian and Hindu–Arabic numerals. However, they were conceptually distinct from these later systems, as they were not used as a positional system with a zero. Rather, there were separate numerals for each of the tens (10, 20, 30, etc.). There were also symbols for 100 and 1000 which were combined in ligatures with the units to signify 200, 300, 2000, 3000, etc.

Evolution of Brahmi numerals from the time of Ashoka.

The number "256" in Ashoka's Minor Rock Edict No.1 in Sasaram (circa 250 BCE).

Coin of Western Satrap Damasena (232 CE). The minting date, here 153 (100-50-3 in Brahmi script numerals) of the Saka era, therefore 232 CE, clearly appears behind the head of the king.

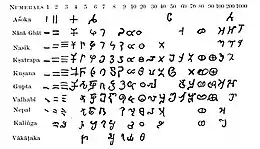
Origins

Brahmi numerals signs of the 2nd century CE.

The source of the first three numerals seems clear: they are collections of 1, 2, and 3 strokes, in Ashoka's era vertical I, II, III like Roman numerals, but soon becoming horizontal like the ancient Han Chinese numerals. In the oldest inscriptions, 4 is a +, reminiscent of the X of neighboring Kharoṣṭhī, and perhaps a representation of 4 lines or 4 directions. However, the other unit numerals appear to be arbitrary symbols in even the oldest inscriptions. It is sometimes supposed that they may also have come from collections of strokes, run together in cursive writing in a way similar to that attested in the development of Egyptian hieratic and demotic numerals, but this is not supported by any direct evidence. Likewise, the units for the tens are not obviously related to each other or to the units, although 10, 20, 80, 90 might be based on a circle.

The sometimes rather striking graphic similarity they have with the hieratic and demotic Egyptian numerals, while suggestive, is not prima facie evidence of an historical connection, as many cultures have independently recorded numbers as collections of strokes. With a similar writing instrument, the cursive forms of such groups of strokes could easily be broadly similar as well, and this is one of the primary hypotheses for the origin of Brahmi numerals.

Another possibility is that the numerals were acrophonic, like the Attic numerals, and based on the Kharoṣṭhī alphabet. For instance, chatur 4 early on took a ¥ shape much like the Kharosthi letter ch; panca 5 looks remarkably like Kharosthi p; and so on through shat 6, sapta 7, and nava 9 (Kharosthi sh, s, n). However, there are problems of timing and lack of records. The full set of numerals is not attested until the 1st-2nd century CE, 400 years after Ashoka. Assertions that either the numerals derive from tallies or that they are alphabetic are, at best, educated guesses.

Numerals

Ancient non-Zero system

Hindu-Arabic numerals	1	2	3	4	5	6	7	8	9	10	20	30	40	50	60	70	80	90	100	1000
Brahmi numerals	𑁒	𑁓	𑁔	𑁕	𑁖	𑁗	𑁘	𑁙	𑁚	𑁛	𑁜	𑁝	𑁞	𑁟	𑁠	𑁡	𑁢	𑁣	𑁤	𑁥

Zero place-holder system

Hindu-Arabic numerals	0	1	2	3	4	5	6	7	8	9
Brahmi numerals	𑁦	𑁧	𑁨	𑁩	𑁪	𑁫	𑁬	𑁭	𑁮	𑁯

See also

• Brahmi script

References

• Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer. Translated by David Bellos, Sophie Wood, pub. J. Wiley, 2000.
• Karl Menninger (mathematics), Number Words and Number Symbols - A Cultural History of Numbers ISBN 0-486-27096-3
• David Eugene Smith and Louis Charles Karpinski, The Hindu-Arabic Numerals (1911)