Brauer algebra

In mathematics, a Brauer algebra is an algebra introduced by Richard Brauer (1937, section 5) used in the representation theory of the orthogonal group. It plays the same role that the symmetric group does for the representation theory of the general linear group in Schur–Weyl duality.

Definition

In terms of diagrams

The product of 2 basis elements A and B of the Brauer algebra with n = 12

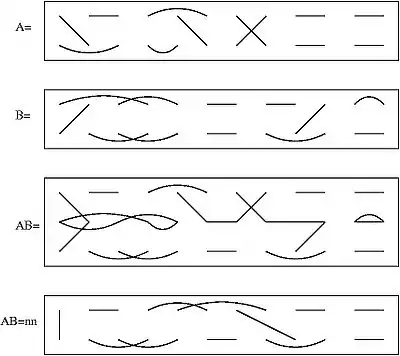
The Brauer algebra ${\displaystyle {\mathfrak {B}}_{n}(\delta )}$ is a ${\displaystyle \mathbb {Z} [\delta ]}$-algebra depending on the choice of a positive integer n. ${\displaystyle d}$ is an indeterminant, but in practice ${\displaystyle \delta }$ is often specialised to the dimension of the fundamental representation of an orthogonal group ${\displaystyle O_{d}(K)}$. The Brauer algebra has dimension ${\displaystyle {\frac {(2n)!}{2^{n}n!}}=(2n-1)(2n-3)\cdots 5\cdot 3\cdot 1}$ and has a basis consisting of all pairings on a set of ${\displaystyle 2n}$ elements ${\displaystyle X_{1},...,X_{n},Y_{1},...,Y_{n}}$ (that is, all perfect matchings of a complete graph ${\displaystyle K_{n}}$: any two of the ${\displaystyle 2n}$ elements may be matched to each other, regardless of their symbols). The elements ${\displaystyle X_{i}}$ are usually written in a row, with the elements ${\displaystyle Y_{i}}$ beneath them. The product of two basis elements ${\displaystyle A}$ and ${\displaystyle B}$ is obtained by first identifying the endpoints in the bottom row of ${\displaystyle A}$ and the top row of ${\displaystyle B}$ (Figure AB in the diagram), then deleting the endpoints in the middle row and joining endpoints in the remaining two rows if they are joined, directly or by a path, in AB (Figure AB=nn in the diagram). Thereby all closed loops in the middle of AB are removed. The product ${\displaystyle A\cdot B}$ of the basis elements is then defined to be the basis element corresponding to the new pairing multiplied by ${\displaystyle \delta ^{r}}$ where ${\displaystyle r}$ is the number of deleted loops. In the example ${\displaystyle A\cdot B=\delta ^{2}AB}$.

In terms of generators and relations

${\displaystyle {\mathfrak {B}}_{n}(\delta )}$ can also be defined as the ${\displaystyle \mathbb {Z} [\delta ]}$-algebra with generators ${\displaystyle s_{1},\ldots ,s_{a-1},e_{1},\ldots ,e_{a-1}}$ satisfying the following relations:

• Relations of the symmetric group:

${\displaystyle s_{i}^{2}=1}$

${\displaystyle s_{i}s_{j}=s_{j}s_{i}}$ whenever ${\displaystyle |i-j|>1}$

${\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}$

• Almost-idempotent relation:

${\displaystyle e_{i}^{2}=\delta e_{i}}$

• Commutation:

${\displaystyle e_{i}e_{j}=e_{j}e_{i}}$

${\displaystyle s_{i}e_{j}=e_{j}s_{i}}$

whenever${\displaystyle |i-j|>1}$

• Tangle relations

${\displaystyle e_{i}e_{i\pm 1}e_{i}=e_{i}}$

${\displaystyle s_{i}s_{i\pm 1}e_{i}=e_{i\pm 1}e_{i}}$

${\displaystyle e_{i}s_{i\pm 1}s_{i}=e_{i}e_{i\pm 1}}$

• Untwisting:

${\displaystyle s_{i}e_{i}=e_{i}s_{i}=e_{i}}$:

${\displaystyle e_{i}s_{i\pm 1}e_{i}=e_{i}}$

In this presentation ${\displaystyle s_{i}}$ represents the diagram in which ${\displaystyle X_{k}}$ is always connected to ${\displaystyle Y_{k}}$ directly beneath it except for ${\displaystyle X_{i}}$ and ${\displaystyle X_{i+1}}$ which are connected to ${\displaystyle Y_{i+1}}$ ans ${\displaystyle Y_{i}}$ respectively. Similarly ${\displaystyle e_{i}}$ represents the diagram in which ${\displaystyle X_{k}}$ is always connected to ${\displaystyle Y_{k}}$ directly beneath it except for ${\displaystyle X_{i}}$ being connected to ${\displaystyle X_{i+1}}$ and ${\displaystyle Y_{i}}$ to ${\displaystyle Y_{i+1}}$.

Properties

The subalgebra generated by the ${\displaystyle s_{i}}$ is the group algebra of the symmetric group. The Brauer algebra is a cellular algebra.

Action on tensor powers

Let ${\displaystyle V}$ be a euclidean vector space of dimension ${\displaystyle d}$. Then write ${\displaystyle B_{n}(d)}$ for the specialisation ${\displaystyle \mathbb {R} \otimes _{\mathbb {Z} [\delta ]}{\mathfrak {B}}_{n}(\delta )}$ where ${\displaystyle \delta }$ acts on ${\displaystyle \mathbb {R} }$ by multiplication with ${\displaystyle d}$. The tensor power ${\displaystyle V^{\otimes n}:=\underbrace {V\otimes \cdots \otimes V} _{a{\text{ times}}}}$ is naturally a ${\displaystyle B_{n}(d)}$-module: ${\displaystyle s_{i}}$ acts by switching the ${\displaystyle i}$th and ${\displaystyle (i+1)}$th tensor factor and ${\displaystyle e_{i}}$ acts by contraction followed by expansion in the ${\displaystyle i}$th and ${\displaystyle (i+1)}$th tensor factor, i.e. ${\displaystyle e_{i}}$ acts as

${\displaystyle v_{1}\otimes \cdots \otimes v_{i-1}\otimes (v_{i}\otimes v_{i+1})\otimes \cdots \otimes v_{n}\mapsto v_{1}\otimes \cdots \otimes v_{i-1}\otimes (\langle v_{i},v_{i+1}\rangle \sum _{k=1}^{d}e_{k}\otimes e_{k})\otimes \cdots \otimes v_{n}}$

where ${\displaystyle e_{1},\ldots ,e_{d}}$ is any orthonormal basis of ${\displaystyle V}$ (the sum is in fact independent of the choice of such a basis).

This action is useful in a generalisation of the Schur-Weyl duality: The image of ${\displaystyle B_{n}(d)}$ inside ${\displaystyle \operatorname {End} (V^{\otimes a})}$ is exactly the centraliser of ${\displaystyle O(V)}$ inside ${\displaystyle \operatorname {End} (V^{\otimes a})}$ and vice versa. The tensor power ${\displaystyle V^{\otimes a}}$ is therefore both an ${\displaystyle O(V)}$- and a ${\displaystyle B_{n}(d)}$-module and satisfies

${\displaystyle V^{\otimes a}=\bigoplus _{\lambda }U_{\lambda }\boxtimes W_{\lambda }}$

where ${\displaystyle \lambda }$ runs over certain partitions and ${\displaystyle U_{\lambda },W_{\lambda }}$ are the irreducible ${\displaystyle O(V)}$- and ${\displaystyle B_{n}(d)}$-module associated with ${\displaystyle \lambda }$ respectively.

The orthogonal group

If O_d(R) is the orthogonal group acting on V = R^d, then the Brauer algebra has a natural action on the space of polynomials on Vⁿ commuting with the action of the orthogonal group.

See also

• Birman–Wenzl algebra, a deformation of the Brauer algebra.

References

• Brauer, Richard (1937), "On Algebras Which are Connected with the Semisimple Continuous Groups", Annals of Mathematics, Second Series, Annals of Mathematics, 38 (4): 857–872, doi:10.2307/1968843, ISSN 0003-486X, JSTOR 1968843
• Wenzl, Hans (1988), "On the structure of Brauer's centralizer algebras", Annals of Mathematics, Second Series, 128 (1): 173–193, doi:10.2307/1971466, ISSN 0003-486X, JSTOR 1971466, MR 0951511
• Weyl, Hermann (1946), The Classical Groups: Their Invariants and Representations, Princeton University Press, ISBN 978-0-691-05756-9, MR 0000255, retrieved 03/2007/26 Check date values in: |access-date= (help)