Carnot's theorem (inradius, circumradius)

In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is

${\displaystyle DF+DG+DH=R+r,\ }$

${\displaystyle {\begin{aligned}&DG+DH+DF\\={}&|DG|+|DH|-|DF|\\={}&R+r\end{aligned}}}$

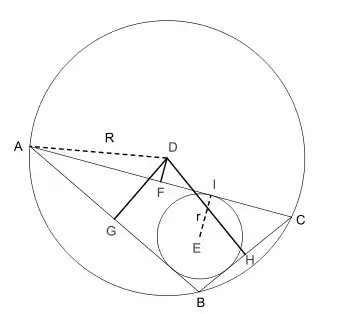
where r is the inradius and R is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment DX (X = F, G, H) lies completely outside the triangle. In the diagram, DF is negative and both DG and DH are positive.

The theorem is named after Lazare Carnot (1753–1823). It is used in a proof of the Japanese theorem for concyclic polygons.

References

• Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009, ISBN 978-0-88385-342-9, p.99
• Frédéric Perrier: Carnot's Theorem in Trigonometric Disguise. The Mathematical Gazette, Volume 91, No. 520 (March, 2007), pp. 115–117 (JSTOR)
• David Richeson: The Japanese Theorem for Nonconvex Polygons – Carnot's Theorem. Convergence, December 2013

External links

• Weisstein, Eric W. "Carnot's theorem". MathWorld.
• Carnot's Theorem at cut-the-knot
• Carnot's Theorem by Chris Boucher. The Wolfram Demonstrations Project.