Circular sector

A circular sector or circle sector (symbol: ⌔), is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector.[1]^:234 In the diagram, θ is the central angle, ${\displaystyle r}$ the radius of the circle, and ${\displaystyle L}$ is the arc length of the minor sector.

The minor sector is shaded in green while the major sector is shaded white.

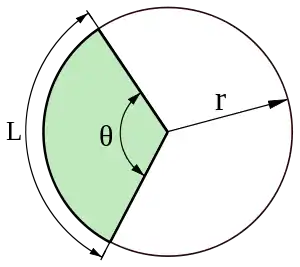
A sector with the central angle of 180° is called a half-disk and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, these include quadrants (90°), sextants (60°) and octants (45°), which come from the sector being one 4th, 6th or 8th part of a full circle, respectively. Confusingly, the arc of a quadrant can also be termed a quadrant.

The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle.[2]^:376

Area

The total area of a circle is πr². The area of the sector can be obtained by multiplying the circle's area by the ratio of the angle θ (expressed in radians) and 2π (because the area of the sector is directly proportional to its angle, and 2π is the angle for the whole circle, in radians):

${\displaystyle A=\pi r^{2}\,{\frac {\theta }{2\pi }}={\frac {r^{2}\theta }{2}}}$

The area of a sector in terms of L can be obtained by multiplying the total area πr² by the ratio of L to the total perimeter 2πr.

${\displaystyle A=\pi r^{2}\,{\frac {L}{2\pi r}}={\frac {rL}{2}}}$

Another approach is to consider this area as the result of the following integral:

${\displaystyle A=\int _{0}^{\theta }\int _{0}^{r}dS=\int _{0}^{\theta }\int _{0}^{r}{\tilde {r}}\,d{\tilde {r}}\,d{\tilde {\theta }}=\int _{0}^{\theta }{\frac {1}{2}}r^{2}\,d{\tilde {\theta }}={\frac {r^{2}\theta }{2}}}$

Converting the central angle into degrees gives[3]

${\displaystyle A=\pi r^{2}{\frac {\theta ^{\circ }}{360^{\circ }}}}$

Perimeter

The length of the perimeter of a sector is the sum of the arc length and the two radii:

${\displaystyle P=L+2r=\theta r+2r=r(\theta +2)}$

where θ is in radians.

Arc length

The formula for the length of an arc is:[4]^:570

${\displaystyle L=r\theta }$

where L represents the arc length, r represents the radius of the circle and θ represents the angle in radians made by the arc at the centre of the circle.[5]^:79

If the value of angle is given in degrees, then we can also use the following formula by:[3]

${\displaystyle L=2\pi r{\frac {\theta }{360}}}$

Chord length

The length of a chord formed with the extremal points of the arc is given by

${\displaystyle C=2R\sin {\frac {\theta }{2}}}$

where C represents the chord length, R represents the radius of the circle, and θ represents the angular width of the sector in radians.

See also

• Circular segment – the part of the sector which remains after removing the triangle formed by the center of the circle and the two endpoints of the circular arc on the boundary.
• Conic section

References

1. Dewan, R. K., Saraswati Mathematics (New Delhi: New Saraswati House, 2016), p. 234.
2. Achatz, T., & Anderson, J. G., with McKenzie, K., ed., Technical Shop Mathematics (New York: Industrial Press, 2005), p. 376.
3. Uppal, Shveta (2019). Mathematics: Textbook for class X. New Delhi: NCERT. pp. 226, 227. ISBN 81-7450-634-9. OCLC 1145113954.
4. Larson, R., & Edwards, B. H., Calculus I with Precalculus (Boston: Brooks/Cole, 2002), p. 570.
5. Wicks, A., Mathematics Standard Level for the International Baccalaureate (West Conshohocken, PA: Infinity, 2005), p. 79.

Sources

• Gerard, L. J. V., The Elements of Geometry, in Eight Books; or, First Step in Applied Logic (London, Longmans, Green, Reader and Dyer, 1874), p. 285.

• Legendre, A. M., Elements of Geometry and Trigonometry, Charles Davies, ed. (New York: A. S. Barnes & Co., 1858), p. 119.