Combustion models for CFD

Combustion models for CFD refers to combustion models for computational fluid dynamics. Combustion is defined as a chemical reaction in which a hydrocarbon fuel reacts with an oxidant to form products, accompanied with the release of energy in the form of heat. Being the integral part of various engineering applications like: internal combustion engines, aircraft engines, rocket engines, furnaces, and power station combustors, combustion manifests itself as a wide domain during the design, analysis and performance characteristics stages of the above-mentioned applications.[1] With the added complexity of chemical kinetics and achieving reacting flow mixture environment, proper modeling physics has to be incorporated during computational fluid dynamic (CFD) simulations of combustion. Hence the following discussion presents a general outline of the various adequate models incorporated with the Computational fluid dynamic code to model the process of combustion.[2]

Overview

Computational fluid dynamics modeling of combustion calls upon the proper selection and implementation of a model suitable to faithfully represent the complex physical and chemical phenomenon associated with any combustion process. The model should be competent enough to deliver information related to the species concentration, their volumetric generation or destruction rate and changes in the parameters of the system like enthalpy, temperature and mixture density. The model should be capable of solving the general transport equations for fluid flow and heat transfer as well as the additional equations of combustion chemistry and chemical kinetics incorporated into that as per the simulating environment desired[1]

Critical considerations in combustion phenomenon

The major consideration during any general combustion process includes the mixing time scale and the reacting time scale elapsed for the process. The flame type and the type of mixing of flow streams of the constituents also have to be taken into account. Apart from that as far as the kinetic complexity of the reaction is concerned, the reaction proceeds in multiple steps and what appears as a simple one line reaction actually completes after a series of reactions.[1][2] Also the transport equations for mass fractions of all the species as well as the enthalpy generated during the reaction have to be solved. Hence even the simplest combustion reaction involves very tedious and rigorous calculation if all the intermediate steps of the combustion process, all transport equations and all flow equations have to be satisfied simultaneously. All these factors will have a significant effect on the computational speed and time of the simulation. But with proper simplifying assumptions Computational fluid dynamic modeling of combustion reaction can be done without substantial compromise on the accuracy and convergence of the solution.[2] The basic models used for the same are covered in the following paragraphs.

Simple chemical reacting system model
Main article: Simple chemical reacting system

This model takes into consideration only the final concentration of species and takes into account only the global nature of combustion process where the reaction proceeds infinitely fast as a single step process without much stress on the detailed kinetics involved.[1]

The reactants are assumed to react in stoichiometric proportions. The model also deduces a linear relationship between the mass fractions of fuel, oxidant and the non dimensional variable mixture fraction.[2] The model also takes into account an additional assumption that the mass diffusion coefficients of all species are equal.[3] Owing to this additional assumption the model only solves one extra partial differential equation for mixture fraction and after solving the transport equation for the mixture fraction the corresponding mass fractions for fuel and oxidant are calculated.

This model can very well be applied to a combustion environment where laminar diffusion effects are dominant and the combustion proceeds via non premixed fuel and oxidant streams diffusing into each other giving rise to a laminar flame.[1]

Eddy break–up model
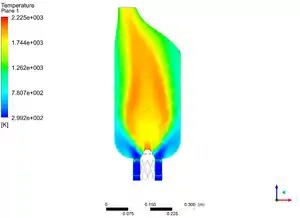
Main article: Eddy break-up model for combustion
Simulation of can combustor using eddy dissipation model.

This model is used when turbulent mixing of the constituents has to be taken into consideration. The k/Ɛ turbulent time scale is used to calculate the reaction rate. A comparison between the turbulent dissipation rates of the fuel, oxidant and products is done and the minimum amongst all is taken as the rate of the reaction. The transport equations for the mass fractions of the constituents are solved using this rate of reaction.[1] Apart from this a mean enthalpy equation is also solved and temperature, density and viscosity are calculated accordingly. The model can also be implemented when finite rate kinetically controlled reaction is to be simulated. In such situation while deciding the rate of the reaction the Arrhenius kinetic rate expression is also taken into account and the rate of reaction is taken as minimum amongst the turbulent dissipation rates of all the constituents and the Arrhenius kinetic rate expression.[2] Since turbulent mixing governs the characteristics of this model, there exists a limit to the quality of the combustion simulation depending upon the type of the turbulent model implemented to represent the flow. The model can also be modified to account for mixing of fine structures during the turbulent reaction. This modification of the model results in the eddy dissipation model which consider the mass fraction of fine structures in its calculations.[1]

Laminar flamelet model
Main article: Laminar flamelet model

This model approximates the turbulent flame as a series of laminar flamelet regions concentrated just around the stoichiometric surfaces of the reacting mixture.[1] This model exploits the use of experimental data for determining relations between the variables considered like mass fraction, temperature etc. The nature and type of dependence of the variables is predicted through experimental data obtained during laminar diffusion flame experiment and laminar flamelet relationship is deduced based on the same. These relationships are then used to solve the transport equations for species mass fraction and mixture composition.[2] The model can very well be implemented for situations where concentration of minor species in the combustion is to be computed like quantifying the generation of pollutants.[1] A simple enhancement to the model results in the flamelet time scale model which takes finite rate kinetics effect into consideration. The flamelet time scale model produces steady laminar flamelet solution when reaction proceeds very fast and captures the finite rate effects when reaction chemistry is dominant.[4]

Presumed probability distribution function model

This model takes into account a statistical approach for calculating the variables like species mass fractions, temperature and density while the mixture composition is calculated at the grids.[2] Then these all variables are calculated as functions of the mixture fraction around a presumed probability distribution function.[1][5] The model can produce satisfactory results for turbulent reactive flows where convection effects due to mean and fluctuating components of velocity are dominant.[6] The model can be extended for adiabatic as well as non adiabatic conditions.

Conditional moment closure

Conditional moment closure (CMC) is an advanced combustion model. The basic idea is to model the chemical source based on conditional averages. The model was first introduced for non-premixed flows and hence the conditioning is done in the mixture fraction.[7]

Other models

The following are some of the other relevant models used for computational fluid dynamic modeling of combustion.

The chemical equilibrium model considers the effect of intermediate reactions during turbulent combustion.[1] The concentration of species is calculated when the combustion reaction reaches equilibrium state. The species concentration is calculated as a function of mixture fraction by deploying certain equilibrium calculation programs available to serve the purpose. The conditional closure model solves the transport equations for the mean components of the flow properties without considering the fluctuating composition of the reaction mixture.[6]

References
  1. “An introduction to Computational Fluid Dynamics-- the finite volume method” H.K. Versteeg and W.Malalasekara Pearson Education limited.p.357
  2. An introduction to Computational Fluid Dynamics-- the finite volume method” H.K. Versteeg and W. Malalasekera Longman Group limited.p.210
  3. http://www.cham.co.uk/phoenics/d_polis/d_lecs/general/combust.htm#2
  4. 9-rao-rutland.pdf---“A Flamelet Time Scale combustion model for turbulent combustion in KIVA” Shrikanth Rao and Christopher J. Rutland( Engine Research Center, UW Madison.)
  5. Pope_NACM_91.pdf—“combustion modeling using probability density function methods” S.B.Pope.
  6. Pope_ACAC_97.pdf---“Turbulence Combustion Modelling: fluctuations and chemistry (advanced computation and analysis of combustion: 310-320)” S.B.Pope (Sibley School of Mechanical and Aerospace Engineering Cornell University,Ithaca NY).
  7. Cant, R.S. & Mastorakos, E. An Introduction to Turbulent Reacting Flows. Imperial College Press, London. 2007.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.