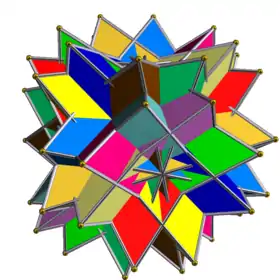
Compound of twelve tetrahedra with rotational freedom

This uniform polyhedron compound is a symmetric arrangement of 12 tetrahedra, considered as antiprisms. It can be constructed by superimposing six identical copies of the stella octangula, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each stella octangula is rotated by an equal (and opposite, within a pair) angle θ. Equivalently, a stella octangula may be inscribed within each cube in the compound of six cubes with rotational freedom, which has the same vertices as this compound.

Compound of twelve tetrahedra with rotational freedom
Type	Uniform compound
Index	UC2
Polyhedra	12 tetrahedra
Faces	48 triangles
Edges	72
Vertices	48
Symmetry group	octahedral (Oh)
Subgroup restricting to one constituent	4-fold improper rotation (S4)

When θ = 0, all six stella octangula coincide. When θ is 45 degrees, the stella octangula coincide in pairs yielding (two superimposed copies of) the compound of six tetrahedra.

Gallery

• Compounds of twelve tetrahedra with rotational freedom
• 
  θ = 0°
• 
  θ = 5°
• 
  θ = 10°
• 
  θ = 15°
• 
  θ = 20°
• 
  θ = 25°
• 
  θ = 30°
• 
  θ = 35°
• 
  θ = 40°
• 
  θ = 45°

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (03): 447–457, doi:10.1017/S0305004100052440, MR 0397554.