Conditional probability distribution

In probability theory and statistics, given two jointly distributed random variables ${\displaystyle X}$ and ${\displaystyle Y}$, the conditional probability distribution of Y given X is the probability distribution of ${\displaystyle Y}$ when ${\displaystyle X}$ is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value ${\displaystyle x}$ of ${\displaystyle X}$ as a parameter. When both ${\displaystyle X}$ and ${\displaystyle Y}$ are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable.

If the conditional distribution of ${\displaystyle Y}$ given ${\displaystyle X}$ is a continuous distribution, then its probability density function is known as the conditional density function. The properties of a conditional distribution, such as the moments, are often referred to by corresponding names such as the conditional mean and conditional variance.

More generally, one can refer to the conditional distribution of a subset of a set of more than two variables; this conditional distribution is contingent on the values of all the remaining variables, and if more than one variable is included in the subset then this conditional distribution is the conditional joint distribution of the included variables.

Conditional discrete distributions

For discrete random variables, the conditional probability mass function of ${\displaystyle Y}$ given ${\displaystyle X=x}$ can be written according to its definition as:

${\displaystyle p_{Y|X}(y\mid x)\triangleq P(Y=y\mid X=x)={\frac {P(\{X=x\}\cap \{Y=y\})}{P(X=x)}}}$

Due to the occurrence of ${\displaystyle P(X=x)}$ in a denominator, this is defined only for non-zero (hence strictly positive) ${\displaystyle P(X=x).}$

The relation with the probability distribution of ${\displaystyle X}$ given ${\displaystyle Y}$ is:

${\displaystyle P(Y=y\mid X=x)P(X=x)=P(\{X=x\}\cap \{Y=y\})=P(X=x\mid Y=y)P(Y=y).}$

Example

Consider the roll of a fair die and let ${\displaystyle X=1}$ if the number is even (i.e. 2, 4, or 6) and ${\displaystyle X=0}$ otherwise. Furthermore, let ${\displaystyle Y=1}$ if the number is prime (i.e. 2, 3, or 5) and ${\displaystyle Y=0}$ otherwise.

	1	2	3	4	5	6
X	0	1	0	1	0	1
Y	0	1	1	0	1	0

Then the unconditional probability that ${\displaystyle X=1}$ is 3/6 = 1/2 (since there are six possible rolls of the die, of which three are even), whereas the probability that ${\displaystyle X=1}$ conditional on ${\displaystyle Y=1}$ is 1/3 (since there are three possible prime number rolls—2, 3, and 5—of which one is even).

Conditional continuous distributions

Similarly for continuous random variables, the conditional probability density function of ${\displaystyle Y}$ given the occurrence of the value ${\displaystyle x}$ of ${\displaystyle X}$ can be written as[1]^{:p. 99}

${\displaystyle f_{Y\mid X}(y\mid x)={\frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

where ${\displaystyle f_{X,Y}(x,y)}$ gives the joint density of ${\displaystyle X}$ and ${\displaystyle Y}$, while ${\displaystyle f_{X}(x)}$ gives the marginal density for ${\displaystyle X}$. Also in this case it is necessary that ${\displaystyle f_{X}(x)>0}$.

The relation with the probability distribution of ${\displaystyle X}$ given ${\displaystyle Y}$ is given by:

${\displaystyle f_{Y\mid X}(y\mid x)f_{X}(x)=f_{X,Y}(x,y)=f_{X|Y}(x\mid y)f_{Y}(y).}$

The concept of the conditional distribution of a continuous random variable is not as intuitive as it might seem: Borel's paradox shows that conditional probability density functions need not be invariant under coordinate transformations.

Example

Bivariate normal joint density

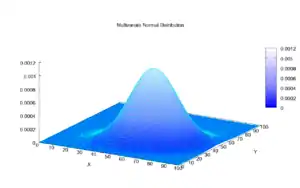
The graph shows a bivariate normal joint density for random variables ${\displaystyle X}$ and ${\displaystyle Y}$. To see the distribution of ${\displaystyle Y}$ conditional on ${\displaystyle X=70}$, one can first visualize the line ${\displaystyle X=70}$ in the ${\displaystyle X,Y}$ plane, and then visualize the plane containing that line and perpendicular to the ${\displaystyle X,Y}$ plane. The intersection of that plane with the joint normal density, once rescaled to give unit area under the intersection, is the relevant conditional density of ${\displaystyle Y}$.

${\displaystyle Y\mid X=70\ \sim \ {\mathcal {N}}\left(\mu _{1}+{\frac {\sigma _{1}}{\sigma _{2}}}\rho (70-\mu _{2}),\,(1-\rho ^{2})\sigma _{1}^{2}\right).}$

Relation to independence

Random variables ${\displaystyle X}$, ${\displaystyle Y}$ are independent if and only if the conditional distribution of ${\displaystyle Y}$ given ${\displaystyle X}$ is, for all possible realizations of ${\displaystyle X}$, equal to the unconditional distribution of ${\displaystyle Y}$. For discrete random variables this means ${\displaystyle P(Y=y|X=x)=P(Y=y)}$ for all possible ${\displaystyle y}$ and ${\displaystyle x}$ with ${\displaystyle P(X=x)>0}$. For continuous random variables ${\displaystyle X}$ and ${\displaystyle Y}$, having a joint density function, it means ${\displaystyle f_{Y}(y|X=x)=f_{Y}(y)}$ for all possible ${\displaystyle y}$ and ${\displaystyle x}$ with ${\displaystyle f_{X}(x)>0}$.

Properties

Seen as a function of ${\displaystyle y}$ for given ${\displaystyle x}$, ${\displaystyle P(Y=y|X=x)}$ is a probability mass function and so the sum over all ${\displaystyle y}$ (or integral if it is a conditional probability density) is 1. Seen as a function of ${\displaystyle x}$ for given ${\displaystyle y}$, it is a likelihood function, so that the sum over all ${\displaystyle x}$ need not be 1.

Additionally, a marginal of a joint distribution can be expressed as the expectation of the corresponding conditional distribution. For instance, ${\displaystyle p_{X}(x)=E_{Y}[p_{X|Y}(X\ |\ Y)]}$.

Measure-theoretic formulation

Let ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ be a probability space, ${\displaystyle {\mathcal {G}}\subseteq {\mathcal {F}}}$ a ${\displaystyle \sigma }$-field in ${\displaystyle {\mathcal {F}}}$, and ${\displaystyle X:\Omega \to \mathbb {R} }$ a real-valued random variable (measurable with respect to the Borel ${\displaystyle \sigma }$-field ${\displaystyle {\mathcal {R}}^{1}}$ on ${\displaystyle \mathbb {R} }$). Given ${\displaystyle A\in {\mathcal {F}}}$, the Radon-Nikodym theorem implies that there is[2] a ${\displaystyle {\mathcal {G}}}$-measurable integrable random variable ${\displaystyle P(A\mid {\mathcal {G}}):\Omega \to \mathbb {R} }$ such that ${\displaystyle \int _{G}P(A\mid {\mathcal {G}})(\omega )dP(\omega )=P(A\cap G)}$ for every ${\displaystyle G\in {\mathcal {G}}}$, and such a random variable is uniquely defined up to sets of probability zero. Further, it can then be shown that there exists[3] a function ${\displaystyle \mu$ :{\mathcal {R}}^{1}\times \Omega \to \mathbb {R} } such that

${\displaystyle \mu (\cdot ,\omega )}$ is a probability measure on ${\displaystyle {\mathcal {R}}^{1}}$ for each ${\displaystyle \omega \in \Omega }$ (i.e., it is regular) and ${\displaystyle \mu (H,\cdot )=P(X^{-1}(H)\mid {\mathcal {G}})}$ (almost surely) for every ${\displaystyle H\in {\mathcal {R}}^{1}}$.

For any ${\displaystyle \omega \in \Omega }$, the function ${\displaystyle \mu (\cdot ,\omega ):{\mathcal {R}}^{1}\to \mathbb {R} }$ is called a conditional probability distribution of ${\displaystyle X}$ given ${\displaystyle {\mathcal {G}}}$. In this case,${\displaystyle E[X\mid {\mathcal {G}}]=\int _{-\infty }^{\infty }x\,\mu (dx,\cdot )}$ almost surely.

Relation to conditional expectation

For any event ${\displaystyle A\in {\mathcal {A}}\supseteq {\mathcal {B}}}$, define the indicator function:

${\displaystyle \mathbf {1} _{A}(\omega )={\begin{cases}1\;&{\text{if }}\omega \in A,\\0\;&{\text{if }}\omega \notin A,\end{cases}}}$

which is a random variable. Note that the expectation of this random variable is equal to the probability of A itself:

${\displaystyle \operatorname {E} (\mathbf {1} _{A})=\operatorname {P} (A).\;}$

Then the conditional probability given ${\displaystyle {\mathcal {B}}}$ is a function ${\displaystyle \operatorname {P} (\cdot \mid {\mathcal {B}}):{\mathcal {A}}\times \Omega \to [0,1]}$ such that ${\displaystyle \operatorname {P} (A\mid {\mathcal {B}})}$ is the conditional expectation of the indicator function for ${\displaystyle A}$:

${\displaystyle \operatorname {P} (A\mid {\mathcal {B}})=\operatorname {E} (\mathbf {1} _{A}\mid {\mathcal {B}})\;}$

In other words, ${\displaystyle \operatorname {P} (A\mid {\mathcal {B}})}$ is a ${\displaystyle {\mathcal {B}}}$-measurable function satisfying

${\displaystyle \int _{B}\operatorname {P} (A\mid {\mathcal {B}})(\omega )\,\mathrm {d} \operatorname {P} (\omega )=\operatorname {P} (A\cap B)\qquad {\text{for all}}\quad A\in {\mathcal {A}},B\in {\mathcal {B}}.}$

A conditional probability is regular if ${\displaystyle \operatorname {P} (\cdot \mid {\mathcal {B}})(\omega )}$ is also a probability measure for all ω ∈ Ω. An expectation of a random variable with respect to a regular conditional probability is equal to its conditional expectation.

• For the trivial sigma algebra ${\displaystyle {\mathcal {B}}=\{\emptyset ,\Omega \}}$ the conditional probability is a constant function, ${\displaystyle \operatorname {P} \!\left(A\mid \{\emptyset ,\Omega \}\right)\equiv \operatorname {P} (A).}$
• For ${\displaystyle A\in {\mathcal {B}}}$, as outlined above, ${\displaystyle \operatorname {P} (A\mid {\mathcal {B}})=1_{A}.}$

See also

• Conditioning (probability)
• Conditional probability
• Regular conditional probability
• Bayes' theorem

Notes

1. Park,Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
2. Billingsley (1995), p. 430
3. Billingsley (1995), p. 439

References

• Billingsley, Patrick (1995). Probability and Measure (3rd ed.). New York: John Wiley and Sons.