Gummel–Poon model

The Gummel–Poon model is a model of the bipolar junction transistor. It was first described in an article published by Hermann Gummel and H. C. Poon at Bell Labs in 1970.[1]

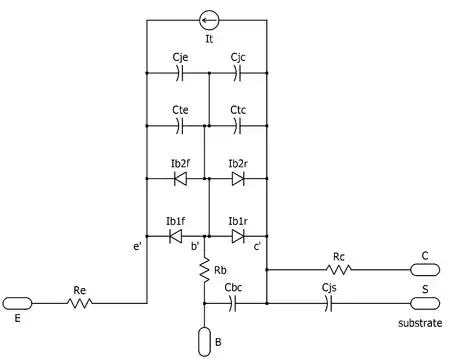
Schematic of Spice Gummel–Poon model NPN

The Gummel–Poon model and modern variants of it are widely used in the popular circuit simulators such as SPICE. A significant effect that the Gummel–Poon model accounts for is the variation of the transistor ${\displaystyle \beta _{\text{F}}}$ and ${\displaystyle \beta _{\text{R}}}$ values with the direct current level. When certain parameters are omitted, the Gummel–Poon model reduces to the simpler Ebers–Moll model.[1]

Model parameters

Spice Gummel–Poon model parameters[2]

#	Name	Property modeled	Parameter	Units	Default value
1	IS	current	transport saturation current	A	1×10^−16
2	BF	current	ideal max. forward beta	—	100
3	NF	current	forward-current emission coefficient	—	1
4	VAF	current	forward early voltage	V	∞
5	IKF	current	corner for forward-beta high-current roll-off	A	∞
6	ISE	current	B–E leakage saturation current	A	0
7	NE	current	B–E leakage emission coefficient	—	1.5
8	BR	current	ideal max. reverse beta	—	1
9	NR	current	reverse-current emission coefficient	—	1
10	VAR	current	reverse early voltage	V	∞
11	IKR	current	corner for reverse-beta high-current roll-off	A	∞
12	ISC	current	B–C leakage saturation current	A	0
13	NC	current	B–C leakage emission coefficient	—	2
14	RB	resistance	zero-bias base resistance	Ω	0
15	IRB	resistance	current where base resistance falls half-way to its minimum	A	∞
16	RBM	resistance	minimum base resistance at high currents	Ω	RB
17	RE	resistance	emitter resistance	Ω	0
18	RC	resistance	collector resistance	Ω	0
19	CJE	capacitance	B–E zero-bias depletion capacitance	F	0
20	VJE	capacitance	B–E built-in potential	V	0.75
21	MJE	capacitance	B–E junction exponential factor	—	0.33
22	TF	capacitance	ideal forward transit time	s	0
23	XTF	capacitance	coefficient for bias dependence of TF	—	0
24	VTF	capacitance	voltage describing VBC dependence of TF	V	∞
25	ITF	capacitance	high-current parameter for effect on TF	A	0
26	PTF		excess phase at frequency = 1/(2π TF)	°	0
27	CJC	capacitance	B–C zero-bias depletion capacitance	F	0
28	VJC	capacitance	B–C built-in potential	V	0.75
29	MJC	capacitance	B–C junction exponential factor	—	0.33
30	XCJC	capacitance	fraction of B–C depletion capacitance connected to internal base node	—	1
31	TR	capacitance	ideal reverse transit time	s	0
32	CJS	capacitance	zero-bias collector–substrate capacitance	F	0
33	VJS	capacitance	substrate–junction built-in potential	V	0.75
34	MJS	capacitance	substrate–junction exponential factor	—	0
35	XTB		forward- and reverse-beta temperature exponent	—	0
36	EG		energy gap for temperature effect of IS	eV	1.1
37	XTI		temperature exponent for effect of IS	—	3
38	KF		flicker-noise coefficient	—	0
39	AF		flicker-noise exponent	—	1
40	FC		coefficient for forward-bias depletion capacitance formula	—	0.5
41	TNOM		parameter measurement temperature	°C	27

See also

• Gummel plot

References

1. H. K. Gummel and H. C. Poon, "An integral charge control model of bipolar transistors", Bell Syst. Tech. J., vol. 49, pp. 827–852, May–June 1970.
2. Summary of model with schematics and equations.

External links

• Bell System Technical Journal, v49: i5 May-June 1970 on archive.org
• Designers-Guide.org comparison paper Xiaochong Cao, J. McMacken, K. Stiles, P. Layman, Juin J. Liou, Adelmo Ortiz-Conde, and S. Moinian, "Comparison of the New VBIC and Conventional Gummel–Poon Bipolar Transistor Models," IEEE Trans-ED 47 #2, Feb. 2000.