Integrator
An integrator in measurement and control applications is an element whose output signal is the time integral of its input signal. It accumulates the input quantity over a defined time to produce a representative output.
Integration is an important part of many engineering and scientific applications. Mechanical integrators are the oldest application, and are still used in such as metering of water flow or electric power. Electronic analogue integrators are the basis of analog computers and charge amplifiers. Integration is also performed by digital computing algorithms.
In signal processing circuits
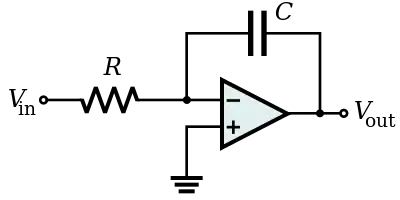
- See also Integrator at op amp applications
An electronic integrator is a form of first-order low-pass filter, which can be performed in the continuous-time (analog) domain or approximated (simulated) in the discrete-time (digital) domain. An integrator will have a low pass filtering effect but when given an offset it will accumulate a value building it until it reaches a limit of the system or overflows.
A voltage integrator is an electronic device performing a time integration of an electric voltage, thus measuring the total volt-second product.
A current integrator is an electronic device performing a time integration of an electric current, thus measuring a total electric charge. A charge amplifier is an example of current integrator. A current integrator is also used to measure the electric charge on a Faraday cup in a residual gas analyzer to measure partial pressures of gasses in a vacuum. Another application of current integration is in ion beam deposition, where the measured charge directly corresponds to the number of ions deposited on a substrate, assuming the charge state of the ions is known. The two current-carrying electrical leads must to be connected to the ion source and the substrate, closing the electric circuit which in part is given by the ion beam.
In software
- Integrators may also be software components.
- In some computational physics computer simulations, such as numerical weather prediction, molecular dynamics, flight simulators, reservoir simulation, noise barrier design, architectural acoustics, and electronic circuit simulation, an integrator is a numerical method for integrating trajectories from forces (and thereby accelerations) that are only calculated at discrete time steps.
Mechanical integrators
Mechanical integrators were key elements in the mechanical differential analyser, used to solve practical physical problems. Mechanical integration mechanisms were also used in control systems such as regulating flows or temperature in industrial processes. Mechanisms such as the ball-and-disk integrator were used both for computation in differential analysers and as components of instruments such as naval gun directors, flow totalizers and others. A planimeter is a mechanical device used for calculating the definite integral of a curve given in graphical form, or more generally finding the area of a closed curve. An integraph is used to plot the indefinite integral of a function given in graphical form.
Drawbacks of ideal integrator
- Bandwidth is very small and used for only small range of input frequencies.
- For dc input (f = 0), the reactance of the capacitance, Xc, is infinite. Because of this op-amp goes into open loop configuration. In open loop configuration the gain is infinite and hence the small input offset voltages are also amplified and appears at output as error. This is referred as false triggering and must be avoided. Due to all such limitations, an ideal integrator needs to be modified. Some additional components are used along with ideal integrator circuit to reduce the effect of an error voltage in practice. This modified integrator is referred as practical integrator.
Practical integrator (lossy integrator)

The gain of an integrator at low frequency can be limited to avoid the saturation problem, therefore to avoid saturation of the op amp the feedback capacitor is shunted by a resistor Rf. The parallel combination of Rf and C behaves like a practical capacitor which dissipates power, unlike an ideal capacitor. For this reason this circuit is also called a lossy integrator. The resistor Rf limits the low frequency gain to (-Rf/R), generally [Rf=10*R1] and thus provides DC stabilisation.
Applications
- Op-amp integrating amplifiers are used to perform calculus operations in analogue computers.
- Integrating circuits are most commonly used in analogue-to-digital converters, ramp generators and also in wave shaping applications.
- Another application would be to integrate a signal representing water flow, producing a signal representing the total quantity of water that has passed by the flow meter. This application of an integrator is sometimes called a totalizer in the industrial instrumentation trade.
See also
References
Further reading
- Keng C. Wu (2002). Transistor Circuits for Spacecraft Power System. Springer. pp. 85–87. ISBN 978-1-4020-7261-1.