Johnson's parabolic formula

In structural engineering, Johnson's parabolic formula is an empirically based equation for calculating the critical buckling stress of a column. The formula is based on experimental results by J. B. Johnson from around 1900 as an alternative to Euler's critical load formula under low slenderness ratio (the ratio of radius of gyration to effective length) conditions. The equation interpolates between the yield stress of the material to the critical buckling stress given by Euler's formula relating the slenderness ratio to the stress required to buckle a column.

Graph of Johnson's parabola (plotted in red) against Euler's formula, with the transition point indicated. The area above the curve indicates failure. The Johnson parabola creates a new region of failure.

Buckling refers to a mode of failure in which the structure loses stability. It is caused by a lack of structural stiffness.[1] Placing a load on a long slender bar may cause a buckling failure before the specimen can fail by compression.[2]

Johnson Parabola

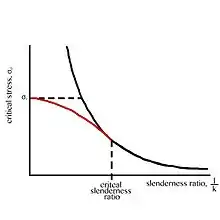
Eulers formula for buckling of a slender column gives the critical stress level to cause buckling but does consider material failure modes such as yield which has been shown to lower the critical buckling stress. Johnson's formula interpolates between the yield stress of the column material and the critical stress given by Euler's formula. It creates a new failure border by fitting a parabola to the graph of failure for Euler buckling using

${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$

There is a transition point on the graph of the Euler curve, located at the critical slenderness ratio. At slenderness values lower than this point (occurring in specimens with a relatively short length compared to their cross section), the graph will follow the Johnson parabola; in contrast, larger slenderness values will align more closely with the Euler equation.

Euler's formula is

${\displaystyle \sigma _{cr}={P_{cr} \over A}={\pi ^{2}EI \over AL_{e}^{2}}={\pi ^{2}E \over \left({\frac {l}{k}}\right)^{2}}}$

where

${\displaystyle \sigma _{cr}=}$ critical stress,

${\displaystyle P_{cr}=}$ critical force,

${\displaystyle A=}$ area of cross section,

${\displaystyle L_{e}=}$ Effective length of the rod,

${\displaystyle E=}$ modulus of elasticity,

${\displaystyle I=}$ area moment of inertia of the cross section of the rod,

${\displaystyle {l \over k}}$ = slenderness ratio.

Euler's equation is useful in situations such as an ideal pinned-pinned column, or in cases in which the effective length can be used to adjust the existing formula (ie. Fixed-Free).[3]

	Pinned-Pinned	Fixed-Fixed	Fixed-Pinned	Fixed-Free
Effective Length, ${\displaystyle L_{e}}$	1L	0.5L	0.7L	2L

(L is the original length of the specimen before the force was applied.)

However, certain geometries are not accurately represented by the Euler formula. One of the variables in the above equation that reflects the geometry of the specimen is the slenderness ratio, which is the column's length divided by the radius of gyration.[4]

The slenderness ratio is an indicator of the specimen's resistance to bending and buckling, due to its length and cross section. If the slenderness ratio is less than the critical slenderness ratio, the column is considered to be a short column. In these cases, the Johnson parabola is more applicable than the Euler formula.[5] The slenderness ratio of the member can be found with ${\displaystyle \left({\frac {l}{k}}\right)=L_{e}{\sqrt {A \over I}}}$

The critical slenderness ratio is

${\displaystyle \left({\frac {l}{k}}\right)_{cr}={\sqrt {2\pi ^{2}E \over \sigma _{y}}}}$

Example

Plot of both Euler and Johnson formulas for Al 2024. The transition point occurs at the critical slenderness ratio.

One common material in aerospace applications is Al 2024. Certain material properties of Al 2024 have been determined experimentally, such as the tensile yield strength (324 MPa) and the modulus of elasticity (73.1 GPa). [6] The Euler formula could be used to plot a failure curve, but it would not be accurate below a certain ${\displaystyle {\frac {l}{k}}}$ value, the critical slenderness ratio.

${\displaystyle {\left({\frac {l}{k}}\right)}_{cr}={\sqrt {2\pi ^{2}E \over \sigma _{y}}}={\sqrt {\frac {2\pi ^{2}\times 73.1\times 10^{9}}{324\times 10^{6}}}}=66.7}$

Therefore, the Euler equation is applicable for values of ${\displaystyle {\frac {l}{k}}}$ greater than 66.7.

Euler: ${\displaystyle \sigma _{cr}={\pi ^{2}E \over \left({\frac {l}{k}}\right)^{2}}={\pi ^{2}\times 73.1\times 10^{9} \over \left({\frac {l}{k}}\right)^{2}}}$ for ${\displaystyle {\frac {l}{k}}>66.7}$

(units in Pascals)

Johnson's parabola takes care of the smaller ${\displaystyle {\frac {l}{k}}}$ values.

Johnson: ${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}=324\times 10^{6}-{1 \over 73.1\times 10^{9}}{\left({\frac {324\times 10^{6}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$ for ${\displaystyle 0\leq {\frac {l}{k}}\leq 66.7}$

(units in Pascals)

References

1. Rice University (2009). "Buckling Analysis". Retrieved from https://www.clear.rice.edu/mech403/HelpFiles/FEA_Buckling_analysis.pdf
2. Dornfeld, W (27 October 2016. "Machine Design". Fairfield University. Retrieved from http://www.faculty.fairfield.edu/wdornfeld/ME311/ME311MachineDesignNotes07.pdf
3. MechaniCalc (2016). "Column Buckling". Retrieved from https://mechanicalc.com/reference/column-buckling
4. Bello, D (2016). "Buckling". Allan Hancock College. Retrieved from http://www.ah-engr.com/som/10_buckling/text_10-1.htm
5. Engineers Edge (2016). "Ideal Pinned Column Buckling Calculation and Equation". Retrieved from http://www.engineersedge.com/column_buckling/column_ideal.htm
6. CRP Meccanica. "Aluminum 2024-T4". Retrieved from http://www.crpmeccanica.com/PDF/aluminium-2024-t4-2024-t351.pdf