Magnetic diffusion
Magnetic diffusion refers to the motion of magnetic field lines, typically in the presence of a conducting solid or fluid such as a plasma. The motion of magnetic fields is described by the magnetic diffusion equation and is due primarily to induction and diffusion of magnetic fields through the material. The magnetic diffusion equation is a partial differential equation commonly used in physics. Understanding the phenomenon is essential to magnetohydrodynamics and has important consequences in astrophysics, geophysics, and electrical engineering.
Equation
The magnetic diffusion equation is
where is the permeability of free space and is the electrical conductivity of the material, which is assumed to be constant. denotes the (non-relativistic) velocity of the plasma. The first term on the right hand side accounts for effects from induction of the plasma, while the second accounts for diffusion. The later acts as a dissipation term, resulting in a loss of magnetic field energy to heat. The relative importance of the two terms is characterized by the magnetic Reynolds number, .
In the case of a non-uniform conductivity the magnetic diffusion equation is
however, it becomes significantly harder to solve.
Derivation
Starting from the generalized Ohm's law:[1][2]
and the curl equations for small displacement currents (i.e. low frequencies)
substitute into the Ampere-Maxwell law to get
- .
Taking the curl of the above equation and substituting into Faraday's law,
- .
This expression can be simplified further by writing it in terms of the i-th component of and the Levi-Cevita tensor :
Using the identity[3] and recalling , the cross products can be eliminated:
Written in vector form, the final expression is
where is the material derivative. This can be rearranged into a more useful form using vector calculus identities and :
In the case , this becomes a diffusion equation for the magnetic field,
where is the magnetic diffusivity.
Limiting Cases
In some cases it is possible to neglect one of the terms in the magnetic diffusion equation. This is done by estimating the magnetic Reynolds number
where is the diffusivity, is the magnitude of the plasma's velocity and is a characteristic length of the plasma.
| Physical Condition | Dominating Term | Magnetic Diffusion Equation | Examples | |
|---|---|---|---|---|
| Large electrical conductivity, large length scales or high plasma velocity. | The inductive term dominates in this case. The motion of magnetic fields is determined by the flow of the plasma. This is the case for most naturally occurring plasmas in the universe. | The Sun or the core of the earth | ||
| Small electrical conductivity, small length scales or low plasma velocity. | The diffusive term dominates in this case. The motion of the magnetic field obeys the typical (nonconducting) fluid diffusion equation. | Solar flares or created in laboratories using mercury or other liquid metals. |
Relation to Skin Effect
At low frequencies, the skin depth for the penetration of an AC electromagnetic field into a conductor is:
Comparing with the formula for , the skin depth is the diffusion length of the field over one period of oscillation:
Examples and Visualization
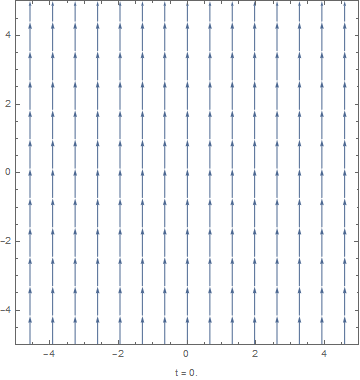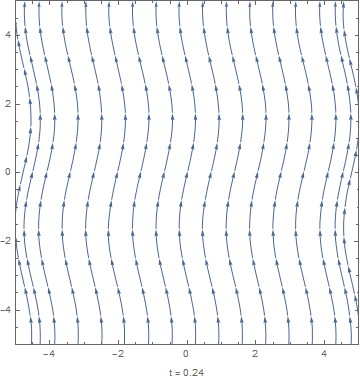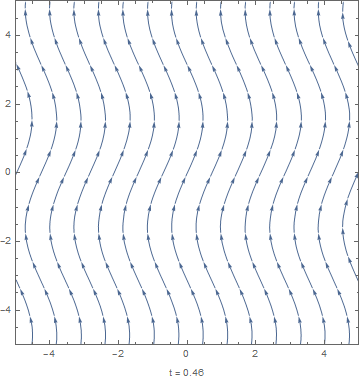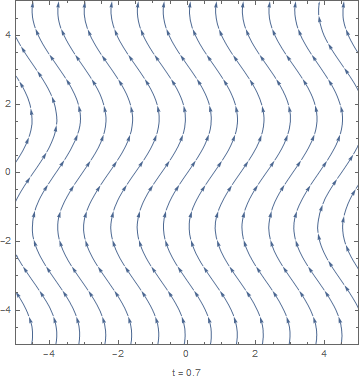
For the limit , the magnetic field lines become "frozen in" to the motion of the conducting fluid. A simple example illustrating this behavior has a sinusoidally-varying shear flow
with a uniform initial magnetic field . The equation for this limit, , has the solution[4]
As can be seen in the figure to the right, the fluid drags the magnetic field lines so that they obtain the sinusoidal character of the flow field.
For the limit , the magnetic diffusion equation is just a vector-valued form of the heat equation. For a localized initial magnetic field (e.g. Gaussian distribution) within a conducting material, the maxima and minima will asymptotically decay to a value consistent with Laplace's equation for the given boundary conditions. This behavior is illustrated in the figure below.
Diffusion Times for Stationary Conductors
For stationary conductors with simple geometries a time constant called magnetic diffusion time can be derived <ref>Brauer, J. R. (2014). Magnetic Actuators and Sensors (2nd ed.). Hoboken NJ: Wiley IEEE Press. ISBN 978-1-118-50525-0.. Different one-dimensional equations apply for conducting slabs and conducting cylinders with constant magnetic permeability. Also, different diffusion time equations can be derived for nonlinear saturable materials such as steel.
References
- Holt, E. H.; Haskell, R. E. (1965). Foundations of Plasma Dynamics. New York: Macmillan. pp. 429-431.
- Chen, Francis F. (2016). Introduction to Plasma Physics and Controlled Fusion (3rd ed.). Heidelberg: Springer. pp. 192–194. ISBN 978-3-319-22308-7.
- Landau, L. D.; Lifshitz, E. M. (2013). The Classical Theory of Fields (4th revised ed.). New York: Elsevier. ISBN 9781483293288.
- Longcope, Dana (2002). "Notes on Magnetohydrodynamics" (PDF). Montana State University - Department of Physics. Retrieved 30 April 2019.