Maurer rose
In geometry, the concept of a Maurer rose was introduced by Peter M. Maurer in his article titled A Rose is a Rose.... A Maurer rose consists of some lines that connect some points on a rose curve.
.svg.png.webp)
A Maurer rose with n = 7 and d = 29
Definition
Let r = sin(nθ) be a rose in the polar coordinate system, where n is a positive integer. The rose has n petals if n is odd, and 2n petals if n is even.
We then take 361 points on the rose:
- (sin(nk), k) (k = 0, d, 2d, 3d, ..., 360d),
where d is a positive integer and the angles are in degrees, not radians.
Explanation
A Maurer rose of the rose r = sin(nθ) consists of the 360 lines successively connecting the above 361 points. Thus a Maurer rose is a polygonal curve with vertices on a rose.
A Maurer rose can be described as a closed route in the polar plane. A walker starts a journey from the origin, (0, 0), and walks along a line to the point (sin(nd), d). Then, in the second leg of the journey, the walker walks along a line to the next point, (sin(n·2d), 2d), and so on. Finally, in the final leg of the journey, the walker walks along a line, from (sin(n·359d), 359d) to the ending point, (sin(n·360d), 360d). The whole route is the Maurer rose of the rose r = sin(nθ). A Maurer rose is a closed curve since the starting point, (0, 0) and the ending point, (sin(n·360d), 360d), coincide.
The following figure shows the evolution of a Maurer rose (n = 2, d = 29°).
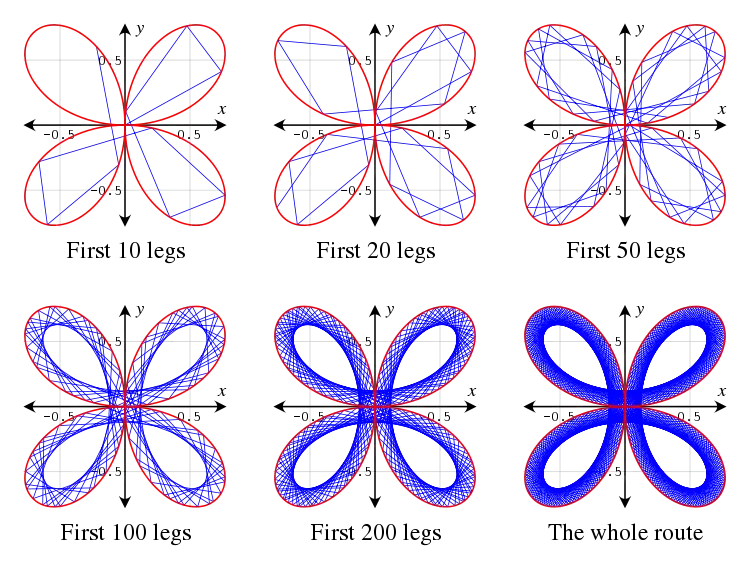
Images
The following are some Maurer roses drawn with some values for n and d:
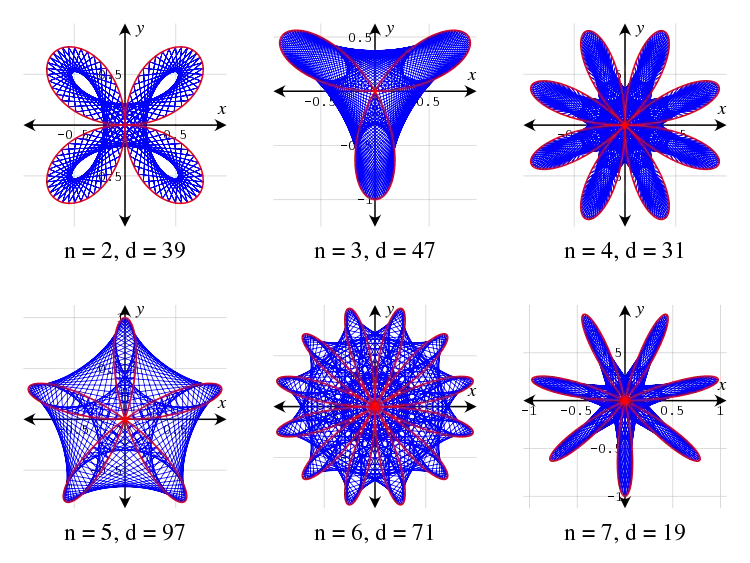
Syntax examples
JavaScript code
// Boilerplate, gotta be somewhere, right?
document.body.innerHTML = ''; // Strips the page of its stuff, in case you just want to paste this into the console in a new tab or really anywhere.
const canv = document.createElement('canvas');
canv.width = 800;
canv.height = 800;
document.body.appendChild(canv);
const ctx = canv.getContext('2d');
// Alright, rose time.
let n = 6, d = 71; // These can be any combination, but this one is nice.
ctx.translate(canv.width / 2, canv.height / 2);
ctx.beginPath();
ctx.lineWidth = 0.5;
ctx.strokeStyle = 'blue';
for (let theta = 0; theta <= 360 /* we're working with degrees, remember? */; theta++){
let k = theta * d * Math.PI / 180;
let r = 300 * Math.sin(n * k);
let x = -r * Math.cos(k);
let y = -r * Math.sin(k);
ctx.lineTo(x, y);
ctx.moveTo(x, y);
}
ctx.stroke();
ctx.beginPath();
ctx.lineWidth = 4;
ctx.strokeStyle = 'red';
for (let theta = 0; theta <= 360; theta++){
let k = theta * Math.PI / 180;
let r = 300 * Math.sin(n * k);
let x = r * Math.cos(k);
let y = -r * Math.sin(k);
ctx.lineTo(x, y);
ctx.moveTo(x, y);
}
ctx.stroke();
Java code
There's a better way to do this. But this is a whole Java file that draws the Maurer rose.
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
class Renderer extends JPanel {
protected void paintComponent(Graphics g) {
Maurer.maurer.draw((Graphics2D) g);
}
}
public class Maurer implements ActionListener {
static Maurer maurer;
static final int width = 800, height = 800;
Renderer renderer = new Renderer();
static double n = 6, d = 71;
public Maurer() {
JFrame frame = new JFrame("maurer rose");
frame.setSize(width, height);
frame.add(renderer);
frame.setDefaultCloseOperation(3);
frame.setResizable(false);
frame.setVisible(true);
Timer timer = new Timer(0, this);
timer.start();
}
public void actionPerformed(ActionEvent evt) {
renderer.repaint();
}
public void draw(Graphics2D g) {
g.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
g.setColor(Color.white);
g.fillRect(0, 0, width, height);
g.setColor(new Color(0, 0, 255, 100));
g.translate(width / 2, height / 2);
double x = 0, y = 0;
for (int theta = 0; theta <= 360; theta++) {
double k = theta * d * Math.PI / 180;
double r = 300 * Math.sin(n * k);
double newX = r * Math.cos(k);
double newY = r * Math.sin(k);
g.drawLine((int)x, (int)y, (int)newX, (int)newY);
x = newX;
y = newY;
}
g.setColor(Color.red);
g.setStroke(new BasicStroke(4));
for (int theta = 0; theta <= 360; theta++) {
double k = theta * Math.PI / 180;
double r = 300 * Math.sin(n * k);
double newX = r * Math.cos(k);
double newY = r * Math.sin(k);
g.drawLine((int)x, (int)y, (int)newX, (int)newY);
x = newX;
y = newY;
}
}
public static void main(String[] args) {
maurer = new Maurer();
}
}
Visual Basic 6 code
n = 7; d = 29 Xo = 400 'Origin Yo = 350 pi = 22 / 7 DrawWidth = 1 For theta = 0 To 360 k = theta * d * pi / 180 r = 300 * Sin(n * k) x = Xo - r * Cos(k) y = Yo - r * Sin(k) Line -(x, y), QBColor(9) Next DrawWidth = 2 For theta = 0 To 360 k = theta * pi / 180 r = 300 * Sin(n * k) x = Xo + r * Cos(k) y = Yo - r * Sin(k) Line -(x, y), QBColor(12) Next
Processing code
float n = 6;
float d = 71;
size(800, 800);
noFill();
background(255);
beginShape();
stroke(0, 0, 255);
strokeWeight(0.5);
for(int theta = 0; theta <= 360; theta++){
float k = theta * d * PI / 180;
float r = 300 * sin(n * k);
float x = r * cos(k) + width/2;
float y = r * sin(k) + height/2;
vertex(x, y);
}
endShape();
beginShape();
stroke(255, 0, 0);
strokeWeight(4);
for(int theta = 0; theta <= 360; theta++){
float k = theta * PI / 180;
float r = 300 * sin(n * k);
float x = r * cos(k) + width/2;
float y = r * sin(k) + height/2;
vertex(x, y);
}
endShape();
p5.js Code
/*p5.js is a port of Processing that can be run in the browser. By going to editor.p5js.org, clearing the code there, pasting this in, and pressing the Play button, you can run it.
A user interface was added so they can select the values of "n" and "d" and also change the formula from sin to any of the 6 basic trig functions (Note: only the sine funcion is a valid Maurer Rose)*/
let n;
let d;
function setup() {
createCanvas(400, 400);
//sets up the slider for n
sliderPetals = createSlider(1,100,6);
sliderPetals.style('width', '300px');
sliderPetals.position(30,height+5);
//sets up the slider for d
sliderD = createSlider(1,360,71);
sliderD.style('width', '300px');
sliderD.position(30,height+30);
//sets up the radio options for the angle formula
angleOptions = createRadio();
angleOptions.position(10, 460);
angleOptions.option('sin');
angleOptions.option('cos');
angleOptions.option('tan');
angleOptions.option('sec');
angleOptions.option('csc');
angleOptions.option('cot');
angleOptions.style('width', '60px');
//reduces the number of calculations your browser has to do
frameRate(3);
}
function draw() {
n = sliderPetals.value();
d = sliderD.value();
background(255);
push();
noFill();
beginShape();
stroke(0, 0, 255);
strokeWeight(0.5);
angleMode(DEGREES);
translate(width/2, height/2);
for(let theta = 0; theta <= 360; theta++){
let k = theta * d;
let r = width/2 * angleFormula(n,k);
let x = r * cos(k);
let y = r * sin(k);
vertex(x, y);
}
endShape();
beginShape();
stroke(255, 0, 0);
strokeWeight(2);
for(let theta = 0; theta <= 360; theta++){
let k = theta;
let r = width/2 * angleFormula(n,k);
let x = r * cos(k);
let y = r * sin(k);
vertex(x, y);
}
endShape();
pop();
stroke(255);
textFont('Georgia', 20);
text('N (#Petals): ' + str(n), 10,20);
text('D :' + str(d), 10, 50);
}
function angleFormula(n,k) {
switch(angleOptions.value()) {
case "sin":
return sin(k*n);
case "cos":
return cos(k*n);
case "tan":
return tan(k*n);
case "csc":
return (1/sin(k*n));
case "sec":
return (1/cos(k*n));
case "cot":
return (1/tan(k*n));
default:
return sin(k*n);
}
}
Python code
Python isn't very efficient when it comes to drawing, so it takes a while. But, the rose won't be upside down like it would in most other languages thanks to Turtle Graphics' ways.
import math, turtle
screen = turtle.Screen()
screen.setup(width=800, height=800, startx=0, starty=0)
screen.bgcolor('black')
pen = turtle.Turtle()
pen.speed(20)
n = 5
d = 97
pen.color('blue')
pen.pensize(0.5)
for theta in range(361):
k = theta * d * math.pi / 180
r = 300 * math.sin(n * k)
x = r * math.cos(k)
y = r * math.sin(k)
pen.goto(x, y)
pen.color('red')
pen.pensize(4)
for theta in range(361):
k = theta * math.pi / 180
r = 300 * math.sin(n * k)
x = r * math.cos(k)
y = r * math.sin(k)
pen.goto(x, y)
C++ code
SFML required
#include "SFML/System.hpp"
#include "SFML/Graphics.hpp"
#include "SFML/Audio.hpp"
#include "SFML/Window.hpp"
#include <iostream>
#include <math.h>
# define M_PI 3.14159265358979323846
int main() {
int n = 6;
int d = 71;
sf::RenderWindow Window(sf::VideoMode(800, 800), "Rose Test", sf::Style::Close );
sf::VertexArray Rose(sf::PrimitiveType::Lines);
sf::VertexArray Outline(sf::PrimitiveType::Lines);
Window.setFramerateLimit(30);
while (Window.isOpen()) {
sf::Event event;
while (Window.pollEvent(event))
{
switch (event.type)
{
case sf::Event::Closed:
Window.close();
break;
}
}
for (int i = 0; i <= 360; i++)
{
double k = i * d * M_PI / 180;
double r = 300 * sin(n * k);
double x = -r * cos(k);
double y = -r * sin(k);
Rose.append(sf::Vertex(sf::Vector2f(x + Window.getSize().x / 2, y + Window.getSize().y / 2), sf::Color::Blue));
}
for (int i = 0; i <= 360; i++)
{
double k = i * M_PI / 180;
double r = 300 * sin(n * k);
double x = r * cos(k);
double y = -r * sin(k);
Outline.append(sf::Vertex(sf::Vector2f(x + Window.getSize().x / 2, y + Window.getSize().y / 2), sf::Color::Red));
}
Window.clear(sf::Color::White);
Window.draw(Rose);
Window.draw(Outline);
Window.display();
}
return 0;
}
References
- Maurer, Peter M. (August–September 1987). "A Rose is a Rose..." The American Mathematical Monthly. 94 (7): 631–645. doi:10.2307/2322215. JSTOR 2322215.
- Weisstein, Eric W. "Maurer roses". MathWorld. (Interactive Demonstrations)
External links
Interactive Demonstration: https://codepen.io/Igor_Konovalov/full/ZJwPQv/ Music player : https://labo86.fr/
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.