Meyer wavelet

The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer.[1] As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters,[2] fractal random fields,[3] and multi-fault classification.[4]

Spectrum of the Meyer wavelet (numerically computed).

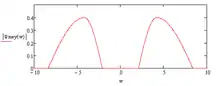
The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function ${\displaystyle \nu }$ as

${\displaystyle \Psi (\omega ):={\begin{cases}{\frac {1}{\sqrt {2\pi }}}\sin \left({\frac {\pi }{2}}\nu \left({\frac {3|\omega |}{2\pi }}-1\right)\right)e^{j\omega /2}&{\text{if }}2\pi /3<|\omega |<4\pi /3,\\{\frac {1}{\sqrt {2\pi }}}\cos \left({\frac {\pi }{2}}\nu \left({\frac {3|\omega |}{4\pi }}-1\right)\right)e^{j\omega /2}&{\text{if }}4\pi /3<|\omega |<8\pi /3,\\0&{\text{otherwise}},\end{cases}}}$

where

${\displaystyle \nu (x):={\begin{cases}0&{\text{if }}x<0,\\x&{\text{if }}0<x<1,\\1&{\text{if }}x>1.\end{cases}}}$

There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts

${\displaystyle \nu (x):={\begin{cases}x^{4}(35-84x+70x^{2}-20x^{3})&{\text{if }}0<x<1,\\0&{\text{otherwise}}.\end{cases}}}$

Meyer scale function (numerically computed)

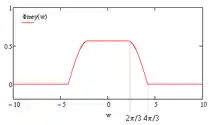
The Meyer scale function is given by

${\displaystyle \Phi (\omega ):={\begin{cases}{\frac {1}{\sqrt {2\pi }}}&{\text{if }}|\omega |<2\pi /3,\\{\frac {1}{\sqrt {2\pi }}}\cos \left({\frac {\pi }{2}}\nu \left({\frac {3|\omega |}{2\pi }}-1\right)\right)&{\text{if }}2\pi /3<|\omega |<4\pi /3,\\0&{\text{otherwise}}.\end{cases}}}$

In the time domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:

waveform of the Meyer wavelet (numerically computed)

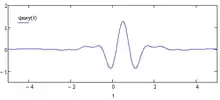
Close expressions

Valenzuela and de Oliveira [5] give the explicit expressions of Meyer wavelet and scale functions:

${\displaystyle \phi (t)={\begin{cases}{\frac {2}{3}}+{\frac {4}{3\pi }}&t=0,\\{\frac {\sin({\frac {2\pi }{3}}t)+{\frac {4}{3}}t\cos({\frac {4\pi }{3}}t)}{\pi t-{\frac {16\pi }{9}}t^{3}}}&{\text{otherwise}},\end{cases}}}$

and

${\displaystyle \psi (t)=\psi _{1}(t)+\psi _{2}(t),}$

where

${\displaystyle \psi _{1}(t)={\frac {{\frac {4}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {2\pi }{3}}(t-{\frac {1}{2}})]-{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {16}{9}}(t-{\frac {1}{2}})^{3}}},}$

${\displaystyle \psi _{2}(t)={\frac {{\frac {8}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {8\pi }{3}}(t-{\frac {1}{2}})]+{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {64}{9}}(t-{\frac {1}{2}})^{3}}}.}$

References

1. Meyer, Yves (1990). Ondelettes et opérateurs: Ondelettes. Hermann. ISBN 9782705661250.
2. Xu, L.; Zhang, D.; Wang, K. (2005). "Wavelet-based cascaded adaptive filter for removing baseline drift in pulse waveforms". IEEE Transactions on Biomedical Engineering. 52 (11): 1973–1975. doi:10.1109/tbme.2005.856296. hdl:10397/193. PMID 16285403.
3. Elliott, Jr., F. W.; Horntrop, D. J.; Majda, A. J. (1997). "A Fourier-Wavelet Monte Carlo method for fractal random fields". Journal of Computational Physics. 132 (2): 384–408. Bibcode:1997JCoPh.132..384E. doi:10.1006/jcph.1996.5647.
4. Abbasion, S.; et al. (2007). "Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine". Mechanical Systems and Signal Processing. 21 (7): 2933–2945. Bibcode:2007MSSP...21.2933A. doi:10.1016/j.ymssp.2007.02.003.
5. Valenzuela, Victor Vermehren; de Oliveira, H. M. (2015). "Close expressions for Meyer Wavelet and Scale Function". Anais de XXXIII Simpósio Brasileiro de Telecomunicações. p. 4. arXiv:1502.00161. doi:10.14209/SBRT.2015.2.

• Daubechies, Ingrid (September 1992). Ten Lectures on Wavelets (CBMS-NSF conference series in applied mathematics) (SIAM ed.). Springer-Verlag. pp. 117–119, 137–138, 152–155. ISBN 978-0-89871-274-2.

External links

• wavelet toolbox
• Matlab implementation