Microseism

In seismology, a microseism is defined as a faint earth tremor caused by natural phenomena.[1][2] Sometimes referred to as a "hum",[3] it should not be confused with the anomalous acoustic phenomenon of the same name. The term is most commonly used to refer to the dominant background seismic and electromagnetic noise signals on Earth, which are caused by water waves in the oceans and lakes.[4][5][6][7][8] Characteristics of microseism are discussed by Bhatt.[8] Because the ocean wave oscillations are statistically homogenous over several hours, the microseism signal is a long-continuing oscillation of the ground.[9] The most energetic seismic waves that make up the microseismic field are Rayleigh waves, but Love waves can make up a significant fraction of the wave field, and body waves are also easily detected with arrays. Because the conversion from the ocean waves to the seismic waves is very weak, the amplitude of ground motions associated to microseisms does not generally exceed 10 micrometers.

Detection and characteristics

Microseisms are very well detected and measured by means of a broad-band seismograph, and can be recorded anywhere on Earth.

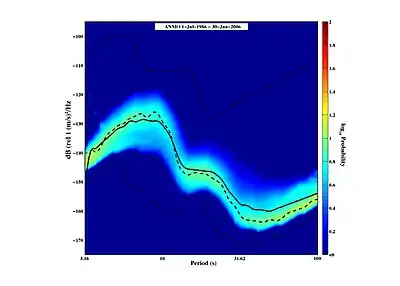
Power spectral density probability density function (color scale at right) for 20 years of continuous vertical component seismic velocity data recorded at Albuquerque, New Mexico by the ANMO station of the IRIS Consortium/USGS Global.Seismographic Network. The high and low bounds are representative noise limits for seismographs deployed worldwide. The solid and dashed lines indicate the median and mode of the probability density function, respectively.

Dominant microseism signals from the oceans are linked to characteristic ocean swell periods, and thus occur between approximately 4 to 30 seconds.[10] Microseismic noise usually displays two predominant peaks. The weaker is for the larger periods, typically close to 16 s, and can be explained by the effect of surface gravity waves in shallow water. These microseisms have the same period as the water waves that generate them, and are usually called 'primary microseisms'. The stronger peak, for shorter periods, is also due to surface gravity waves in water, but arises from the interaction of waves with nearly equal frequencies but nearly opposite directions (the clapotis). These tremors have a period which is half of the water wave period and are usually called 'secondary microseisms'. A slight, but detectable, incessant excitation of the Earth's free oscillations, or normal modes, with periods in the range 30 to 1000 s, and is often referred to as the "Earth hum". For periods up to 300 s, the vertical displacement corresponds to Rayleigh waves generated like the primary microseisms, with the difference that it involves the interaction of infragravity waves with the ocean bottom topography.[11] The dominant sources of this vertical hum component are likely located along the shelf break, the transition region between continental shelves and the abyssal plains.

As a result, from the short period 'secondary microseisms' to the long period 'hum', this seismic noise contains information on the sea states. It can be used to estimate ocean wave properties and their variation, on time scales of individual events (a few hours to a few days) to their seasonal or multi-decadal evolution. Using these signals, however, requires a basic understanding of the microseisms generation processes.

Generation of primary microseisms

The details of the primary mechanism was first given by Klaus Hasselmann,[5] with a simple expression of the microseism source in the particular case of a constant sloping bottom. It turns out that this constant slope needs to be fairly large (around 5 percent or more) to explain the observed microseism amplitudes, and this is not realistic. Instead, small-scale bottom topographic features do not need to be so steep, and the generation of primary microseisms is more likely a particular case of a wave-wave interaction process in which one wave is fixed, the bottom. To visualize what happens, it is easier to study the propagation of waves over a sinusoidal bottom topography. This is easily generalizes to bottom topography with oscillations around a mean depth.[12]

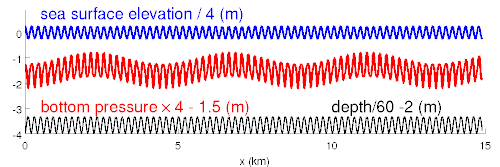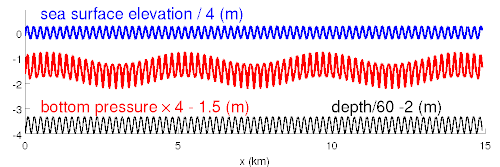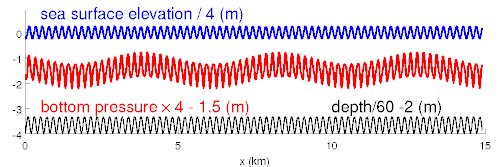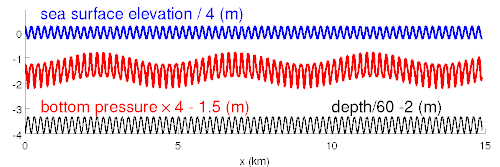
Interference of ocean waves with a fixed bottom topography. Here waves with period 12 s interact with bottom undulations of 205 m wavelength and 20 m amplitude in a mean water depth of 100 m. These conditions give rise to a pressure pattern on the bottom that travels much faster than the ocean waves, and in the direction of the waves if their wavelength L1 is shorter than the bottom wavelength L2, or in the opposite direction if their wavelength is longer, which is the case here. The motion is exactly periodic in time, with the period of the ocean waves. The large wavelength in the bottom pressure is 1/(1/L1 − 1/L2).

For a real bottom, that has a broad spectrum, seismic waves are generated with all wavelengths and in all directions.

Generation of secondary microseisms

The interaction of two trains of surface waves of different frequencies and directions generates wave groups. For wave propagating almost in the same direction, this gives the usual sets of waves that travel at the group speed, which is slower than phase speed of water waves (see animation). For typical ocean waves with a period around 10 seconds, this group speed is close to 10 m/s.

In the case of opposite propagation direction the groups travel at a much larger speed, which is now 2π(f1 + f2)/(k1 − k2) with k1 and k2 the wave numbers of the interacting water waves.

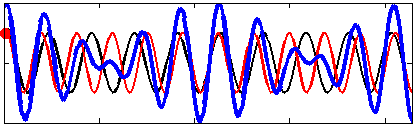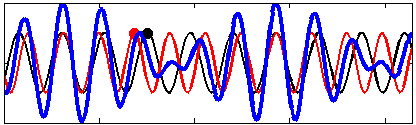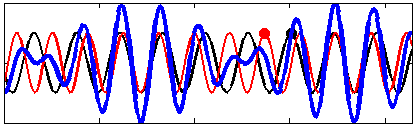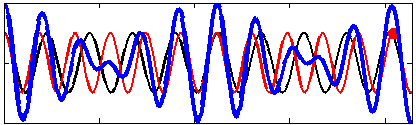
Wave groups generated by waves with same directions. The blue curve is the sum of the red and black. In the animation, watch the crests with the red and black dots. These crests move with the phase speed of linear water waves, and the groups of large waves propagate slower (Animation)

For wave trains with a very small difference in frequency (and thus wavenumbers), this pattern of wave groups may have the same velocity as seismic waves, between 1500 and 3000 m/s, and will excite acoustic-seismic modes that radiate away.

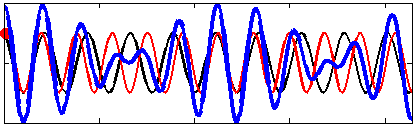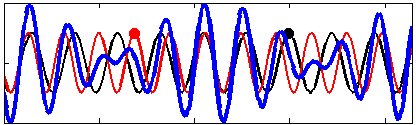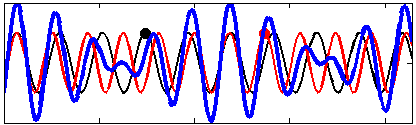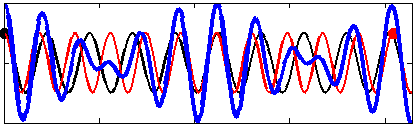
Wave groups generated by waves with opposing directions. The blue curve is the sum of the red and black. In the animation, watch the crests with the red and black dots. These crests move with the phase speed of linear water waves, but the groups propagate much faster (Animation)

As far as seismic and acoustic waves are concerned, the motion of ocean waves in deep water is, to the leading order, equivalent to a pressure applied at the sea surface.[5] This pressure is nearly equal to the water density times the wave orbital velocity squared. Because of this square, it is not the amplitude of the individual wave trains that matter (red and black lines in the figures) but the amplitude of the sum, the wave groups (blue line in figures).

Real ocean waves are composed of an infinite number of wave trains and there is always some energy propagating in the opposite direction. Also, because the seismic waves are much faster than the water waves, the source of seismic noise is isotropic: the same amount of energy is radiated in all directions. In practice, the source of seismic energy is strongest when there are a significant amount of wave energy traveling in opposite directions. This occurs when swell from one storm meets waves with the same period from another storm,[6] or close to the coast due coastal reflection.

Depending on the geological context, the noise recorded by a seismic station on land can be representative of the sea state close to the station (within a few hundred kilometers, for example in Central California), or a full ocean basin (for example in Hawaii).[7] In order to understand the noise properties, it is thus necessary to understand the propagation of the seismic waves.

Rayleigh waves constitute most of the secondary microseismic field. Both water and solid Earth particles are displaced by the waves as they propagate, and the water layer plays a very important role in defining the celerity, group speed and the transfer of energy from the surface water waves to the Rayleigh waves. The generation of secondary-microseism Love waves involves mode conversion by non-planar bathymetry and, internally, through seismic wavespeed homogeneity within the Earth.[13]

See also

References
  1. The American Heritage Dictionary of the English Language (Fourth ed.), Houghton Mifflin Company, 2000
  2. Ebel, John E. (2002), "Watching the Weather Using a Seismograph", Seismological Research Letters, 73 (6): 930–932, doi:10.1785/gssrl.73.6.930.
  3. Ardhuin, Fabrice, Lucia Gualtieri, and Eleonore Stutzmann. "How ocean waves rock the Earth: two mechanisms explain seismic noise with periods 3 to 300 s." Geophys. Res. Lett. 42 (2015).
  4. Longuet-Higgins, M. S. (1950), "A theory of the origin of microseisms", Philosophical Transactions of the Royal Society A, 243 (857): 1–35, Bibcode:1950RSPTA.243....1L, doi:10.1098/rsta.1950.0012, S2CID 31828394
  5. Hasselmann, K. (1963), "A statistical analysis of the generation of micro-seisms", Rev. Geophys., 1 (2): 177–210, Bibcode:1963RvGSP...1..177H, doi:10.1029/RG001i002p00177
  6. Kedar, S.; Longuet-Higgins, M. S.; Graham, F. W. N.; Clayton, R.; Jones, C. (2008), "The origin of deep ocean microseisms in the north Atlantic ocean" (PDF), Proc. Roy. Soc. Lond. A, 464 (2091): 1–35, Bibcode:2008RSPSA.464..777K, doi:10.1098/rspa.2007.0277, S2CID 18073415
  7. Ardhuin, F.; Stutzmann, E.; Schimmel, M.; Mangeney, A. (2011), "Ocean wave sources of seismic noise" (PDF), J. Geophys. Res., 115 (C9): C09004, Bibcode:2011JGRC..116.9004A, doi:10.1029/2011jc006952
  8. Bhatt, Kaushalendra M (2014). "Microseisms and its impact on the marine-controlled source electromagnetic signal". Journal of Geophysical Research: Solid Earth. 119 (12): 2169–9356. Bibcode:2014JGRB..119.8655B. doi:10.1002/2014JB011024.
  9. "Microseism". Retrieved 2008-08-25.
  10. Ruff, L.J. "Hurricane Season & Microseisms". MichSeis. Archived from the original on 2008-05-29. Retrieved 2008-08-26.
  11. Ardhuin, F.; Gualtieri, L.; Stutzmann, E. (2015), "How ocean wagves rock the Earth: two mechanisms explain microseisms with periods 3 to 300 s", Geophys. Res. Lett., 42 (3): 765–772, Bibcode:2015GeoRL..42..765A, doi:10.1002/2014GL062782
  12. Ardhuin, Fabrice. "Large scale forces under surface gravity waves at a wavy bottom: a mechanism for the generation of primary microseisms." Geophys. Res. Lett. 45 (2018), doi: 10.1029/2018GL078855.
  13. Gualtieri, Lucia (9 November 2020). "The origin of secondary microseism Love waves". Proceedings of the National Academy of Sciences. 117 (47): 29504-29511. doi:10.1073/pnas.2013806117.

Sources

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.