Novikov self-consistency principle

The Novikov self-consistency principle, also known as the Novikov self-consistency conjecture and Larry Niven's law of conservation of history, is a principle developed by Russian physicist Igor Dmitriyevich Novikov in the mid-1980s. Novikov intended it to solve the problem of paradoxes in time travel, which is theoretically permitted in certain solutions of general relativity that contain what are known as closed timelike curves. The principle asserts that if an event exists that would cause a paradox or any "change" to the past whatsoever, then the probability of that event is zero. It would thus be impossible to create time paradoxes.

History

Physicists have long known that some solutions to the theory of general relativity contain closed timelike curves—for example the Gödel metric. Novikov discussed the possibility of closed timelike curves (CTCs) in books he wrote in 1975 and 1983,[1] offering the opinion that only self-consistent trips back in time would be permitted.[2] In a 1990 paper by Novikov and several others, "Cauchy problem in spacetimes with closed timelike curves",[3] the authors state:

The only type of causality violation that the authors would find unacceptable is that embodied in the science-fiction concept of going backward in time and killing one's younger self ("changing the past"). Some years ago one of us (Novikov10) briefly considered the possibility that CTCs might exist and argued that they cannot entail this type of causality violation: events on a CTC are already guaranteed to be self-consistent, Novikov argued; they influence each other around a closed curve in a self-adjusted, cyclical, self-consistent way. The other authors recently have arrived at the same viewpoint.

We shall embody this viewpoint in a principle of self-consistency, which states that the only solutions to the laws of physics that can occur locally in the real Universe are those which are globally self-consistent. This principle allows one to build a local solution to the equations of physics only if that local solution can be extended to a part of a (not necessarily unique) global solution, which is well defined throughout the nonsingular regions of the space-time.

Among the co-authors of this 1990 paper were Kip Thorne, Mike Morris, and Ulvi Yurtsever, who in 1988 had stirred up renewed interest in the subject of time travel in general relativity with their paper "Wormholes, Time Machines, and the Weak Energy Condition",[4] which showed that a new general relativity solution known as a traversable wormhole could lead to closed timelike curves, and unlike previous CTC-containing solutions, it did not require unrealistic conditions for the universe as a whole. After discussions with another co-author of the 1990 paper, John Friedman, they convinced themselves that time travel needn't lead to unresolvable paradoxes, regardless of the object sent through the wormhole.[5]:509

"Polchinski's paradox"
Echeverria and Klinkhammer's resolution

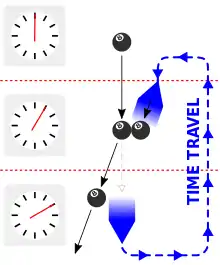
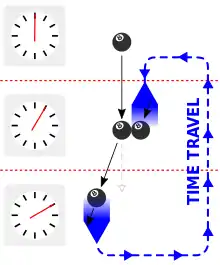
By way of response, physicist Joseph Polchinski wrote them a letter arguing that one could avoid the issue of free will by employing a potentially paradoxical thought experiment involving a billiard ball sent back in time through a wormhole. In Polchinski's scenario, the billiard ball is fired into the wormhole at an angle such that, if it continues along its path, it will exit in the past at just the right angle to collide with its earlier self, knocking it off track and preventing it from entering the wormhole in the first place. Thorne would refer to this scenario as "Polchinski's paradox" in 1994.[6]:510–511

Upon considering the scenario, Fernando Echeverria and Gunnar Klinkhammer, two students at Caltech (where Thorne taught), arrived at a solution to the problem that managed to avoid any inconsistencies. In the revised scenario, the ball emerges from the future at a different angle than the one that generates the paradox, and delivers its younger self a glancing blow instead of knocking it completely away from the wormhole. This blow alters its trajectory by just the right degree, meaning it will travel back in time with the angle required to deliver its younger self the necessary glancing blow. Echeverria and Klinkhammer actually found that there was more than one self-consistent solution, with slightly different angles for the glancing blow in each situation. Later analysis by Thorne and Robert Forward illustrated that for certain initial trajectories of the billiard ball, there could actually be an infinite number of self-consistent solutions.[6]:511–513

Echeverria, Klinkhammer, and Thorne published a paper discussing these results in 1991;[7] in addition, they reported that they had tried to see if they could find any initial conditions for the billiard ball for which there were no self-consistent extensions, but were unable to do so. Thus, it is plausible that there exist self-consistent extensions for every possible initial trajectory, although this has not been proven.[8]:184 This only applies to initial conditions outside of the chronology-violating region of spacetime,[8]:187 which is bounded by a Cauchy horizon.[9] This could mean that the Novikov self-consistency principle does not actually place any constraints on systems outside of the region of space-time where time travel is possible, only inside it.

Even if self-consistent extensions can be found for arbitrary initial conditions outside the Cauchy Horizon, the finding that there can be multiple distinct self-consistent extensions for the same initial condition—indeed, Echeverria et al. found an infinite number of consistent extensions for every initial trajectory they analyzed[8]:184—can be seen as problematic, since classically there seems to be no way to decide which extension the laws of physics will choose. To get around this difficulty, Thorne and Klinkhammer analyzed the billiard ball scenario using quantum mechanics,[6]:514–515 performing a quantum-mechanical sum over histories (path integral) using only the consistent extensions, and found that this resulted in a well-defined probability for each consistent extension. The authors of Cauchy problem in spacetimes with closed timelike curves write:

The simplest way to impose the principle of self-consistency in quantum mechanics (in a classical space-time) is by a sum-over-histories formulation in which one includes all those, and only those, histories that are self-consistent. It turns out that, at least formally (modulo such issues as the convergence of the sum), for every choice of the billiard ball's initial, nonrelativistic wave function before the Cauchy horizon, such a sum over histories produces unique, self-consistent probabilities for the outcomes of all sets of subsequent measurements. ... We suspect, more generally, that for any quantum system in a classical wormhole spacetime with a stable Cauchy horizon, the sum over all self-consistent histories will give unique, self-consistent probabilities for the outcomes of all sets of measurements that one might choose to make.

Assumptions

The Novikov consistency principle assumes certain conditions about what sort of time travel is possible. Specifically, it assumes either that there is only one timeline, or that any alternative timelines (such as those postulated by the many-worlds interpretation of quantum mechanics) are not accessible.

Given these assumptions, the constraint that time travel must not lead to inconsistent outcomes could be seen merely as a tautology, a self-evident truth that can not possibly be false. However, the Novikov self-consistency principle is intended to go beyond just the statement that history must be consistent, making the additional nontrivial assumption that the universe obeys the same local laws of physics in situations involving time travel that it does in regions of space-time that lack closed timelike curves. This is clarified in the above-mentioned "Cauchy problem in spacetimes with closed timelike curves",[3] where the authors write:

That the principle of self-consistency is not totally tautological becomes clear when one considers the following alternative: The laws of physics might permit CTCs; and when CTCs occur, they might trigger new kinds of local physics which we have not previously met. ... The principle of self-consistency is intended to rule out such behavior. It insists that local physics is governed by the same types of physical laws as we deal with in the absence of CTCs: the laws that entail self-consistent single valuedness for the fields. In essence, the principle of self-consistency is a principle of no new physics. If one is inclined from the outset to ignore or discount the possibility of new physics, then one will regard self-consistency as a trivial principle.

Implications for time travelers

The assumptions of the self-consistency principle can be extended to hypothetical scenarios involving intelligent time travelers as well as unintelligent objects such as billiard balls. The authors of "Cauchy problem in spacetimes with closed timelike curves" commented on the issue in the paper's conclusion, writing:

If CTCs are allowed, and if the above vision of theoretical physics' accommodation with them turns out to be more or less correct, then what will this imply about the philosophical notion of free will for humans and other intelligent beings? It certainly will imply that intelligent beings cannot change the past. Such change is incompatible with the principle of self-consistency. Consequently, any being who went through a wormhole and tried to change the past would be prevented by physical law from making the change; i.e., the "free will" of the being would be constrained. Although this constraint has a more global character than constraints on free will that follow from the standard, local laws of physics, it is not obvious to us that this constraint is more severe than those imposed by standard physical law.[3]

Similarly, physicist and astronomer J. Craig Wheeler concludes that:

According to the consistency conjecture, any complex interpersonal interactions must work themselves out self-consistently so that there is no paradox. That is the resolution. This means, if taken literally, that if time machines exist, there can be no free will. You cannot will yourself to kill your younger self if you travel back in time. You can coexist, take yourself out for a beer, celebrate your birthday together, but somehow circumstances will dictate that you cannot behave in a way that leads to a paradox in time. Novikov supports this point of view with another argument: physics already restricts your free will every day. You may will yourself to fly or to walk through a concrete wall, but gravity and condensed-matter physics dictate that you cannot. Why, Novikov asks, is the consistency restriction placed on a time traveler any different?[10]

Time-loop logic
Main article: Time loop

Time-loop logic, coined by roboticist and futurist Hans Moravec,[11] is a hypothetical system of computation that exploits the Novikov self-consistency principle to compute answers much faster than possible with the standard model of computational complexity using Turing machines. In this system, a computer sends a result of a computation backwards through time and relies upon the self-consistency principle to force the sent result to be correct, provided the machine can reliably receive information from the future and provided the algorithm and the underlying mechanism are formally correct. An incorrect result or no result can still be produced if the time travel mechanism or algorithm are not guaranteed to be accurate.

A simple example is an iterative method algorithm. Moravec states:

Make a computing box that accepts an input, which represents an approximate solution to some problem, and produces an output that is an improved approximation. Conventionally you would apply such a computation repeatedly a finite number of times, and then settle for the better, but still approximate, result. Given an appropriate negative delay something else is possible: [...] the result of each iteration of the function is brought back in time to serve as the "first" approximation. As soon as the machine is activated, a so-called "fixed-point" of F, an input which produces an identical output, usually signaling a perfect answer, appears (by an extraordinary coincidence!) immediately and steadily. [...] If the iteration does not converge, that is, if F has no fixed point, the computer outputs and inputs will shut down or hover in an unlikely intermediate state.

Quantum computation with a negative delay

Physicist David Deutsch showed in 1991 that this model of computation could solve NP problems in polynomial time,[12] and Scott Aaronson later extended this result to show that the model could also be used to solve PSPACE problems in polynomial time.[13][14] Deutsch shows that quantum computation with a negative delay—backwards time travel—produces only self-consistent solutions, and the chronology-violating region imposes constraints that are not apparent through classical reasoning.[12] Researchers published in 2014 a simulation in which they claim to have validated Deutsch's model with photons.[15] However, it was shown in an article by Tolksdorf and Verch that Deutsch's self-consistency condition can be fulfilled to arbitrary precision in any quantum system described according to relativistic quantum field theory even on spacetimes which do not admit closed timelike curves, casting doubts on whether Deutsch's model is really characteristic of quantum processes simulating closed timelike curves in the sense of general relativity.[16]

See also

References
  1. See note 10 on p. 42 of Friedman et al., "Cauchy problem in space-times with closed timelike curves"
  2. On p. 169 of Novikov's Evolution of the Universe (1983), which was a translation of his Russian book Evolyutsiya Vselennoĭ (1979), Novikov's comment on the issue is rendered by translator M.M Basko as "The close of time curves does not necessarily imply a violation of causality, since the events along such a closed line may be all 'self-adjusted'—they all affect one another through the closed cycle and follow one another in a self-consistent way."
  3. Friedman, John; Michael Morris; Igor Novikov; Fernando Echeverria; Gunnar Klinkhammer; Kip Thorne; Ulvi Yurtsever (1990). "Cauchy problem in spacetimes with closed timelike curves". Physical Review D. 42 (6): 1915. Bibcode:1990PhRvD..42.1915F. doi:10.1103/PhysRevD.42.1915. PMID 10013039.
  4. Thorne, Kip; Michael Morris; Ulvi Yurtsever (1988). "Wormholes, Time Machines, and the Weak Energy Condition" (PDF). Physical Review Letters. 61 (13): 1446–1449. Bibcode:1988PhRvL..61.1446M. doi:10.1103/PhysRevLett.61.1446. PMID 10038800.
  5. Thorne, Kip S. (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W.W. Norton. pp. 510–. ISBN 978-0-393-31276-8. Polchinski's paradox.
  6. Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. ISBN 0-393-31276-3.
  7. Echeverria, Fernando; Gunnar Klinkhammer; Kip Thorne (1991). "Billiard balls in wormhole spacetimes with closed timelike curves: Classical theory". Physical Review D. 44 (4): 1077. Bibcode:1991PhRvD..44.1077E. doi:10.1103/PhysRevD.44.1077.
  8. Earman, John (1995). Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes. Oxford University Press. ISBN 0-19-509591-X.
  9. Nahin, Paul J. (1999). Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction. American Institute of Physics. p. 508. ISBN 0-387-98571-9.
  10. Wheeler, J. Craig (2007). Cosmic Catastrophes: Exploding Stars, Black Holes, and Mapping the Universe (2nd ed.). Cambridge University Press. pp. 294–295. ISBN 978-0521857147.
  11. Moravec, Hans (1991). "Time Travel and Computing". Archived from the original on 2009-01-29. Retrieved 2008-07-28.
  12. Deutsch, David (1991). "Quantum mechanics near closed timelike lines". Physical Review D. 44 (10): 3197–3217. Bibcode:1991PhRvD..44.3197D. doi:10.1103/PhysRevD.44.3197. PMID 10013776.
  13. Aaronson, Scott (March 2008). "The Limits of Quantum Computers" (PDF). Scientific American: 68–69 – via scottaaronson.com.
  14. Aaronson, Scott; Watrous, John (2009). "Closed Timelike Curves Make Quantum and Classical Computing Equivalent" (PDF). Proceedings of the Royal Society A. 465 (2102): 631–647. arXiv:0808.2669. Bibcode:2009RSPSA.465..631A. doi:10.1098/rspa.2008.0350 – via scottaaronson.com.
  15. Ringbauer, Martin; Broome, Matthew A.; Myers, Casey R.; White, Andrew G.; Ralph, Timothy C. (19 June 2014). "Experimental simulation of closed timelike curves". Nature Communications. 5: 4145. arXiv:1501.05014. Bibcode:2014NatCo...5E4145R. doi:10.1038/ncomms5145. PMID 24942489.
  16. Tolksdorf, Juergen; Verch, Rainer (2018). "Quantum physics, fields and closed timelike curves: The D-CTC condition in quantum field theory". Communications in Mathematical Physics. 357 (1): 319–351. arXiv:1609.01496. Bibcode:2018CMaPh.357..319T. doi:10.1007/s00220-017-2943-5.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.