Painter's algorithm

The painter’s algorithm (also depth-sort algorithm and priority fill) is an algorithm for visible surface determination in 3D computer graphics that works on a polygon-by-polygon basis rather than a pixel-by-pixel, row by row, or area by area basis of other Hidden Surface Removal algorithms.[1][2][3] The painter’s algorithm creates images by sorting the polygons within the image by their depth and placing each polygon in order from the farthest to the closest object.[4][5]

Not to be confused with Schlemiel the Painter's algorithm.

The painter's algorithm was initially proposed as a basic method to address the Hidden-surface determination problem by Martin Newell, Richard Newell, and Tom Sancha in 1972, while all three were working at CADCentre.[4] The name "painter's algorithm" refers to the technique employed by many painters where they begin by painting distant parts of a scene before parts that are nearer, thereby covering some areas of distant parts.[6][7] Similarly, the painter's algorithm sorts all the polygons in a scene by their depth and then paints them in this order, farthest to closest.[8] It will paint over the parts that are normally not visible — thus solving the visibility problem — at the cost of having painted invisible areas of distant objects.[9] The ordering used by the algorithm is called a 'depth order' and does not have to respect the numerical distances to the parts of the scene: the essential property of this ordering is, rather, that if one object obscures part of another, then the first object is painted after the object that it obscures.[9] Thus, a valid ordering can be described as a topological ordering of a directed acyclic graph representing occlusions between objects.[10]

The distant mountains are painted first, followed by the closer meadows; finally, the trees, are painted. Although some trees are more distant from the viewpoint than some parts of the meadows, the ordering (mountains, meadows, trees) forms a valid depth order, because no object in the ordering obscures any part of a later object.

Algorithm

Conceptually Painter’s Algorithm works as follows:

  1. Sort each polygon by depth
  2. Place each polygon from the furthest polygon to the closest polygon

Pseudo-code

 
1  sort polygons by depth
2  for each polygon p:
3      for each pixel that p covers:
4          paint p.color on pixel

Time-Complexity

The painter's algorithm's time-complexity is heavily dependent on the sorting algorithm used to order the polygons. Assuming the use of the most optimal sorting algorithm, painter's algorithm has a worst-case complexity of O(n log n + m*n), where n is the number of polygons and m is the number of pixels to be filled.

Space-Complexity

The painter's algorithm's worst-case space-complexity is O(n+m), where n is the number of polygons and m is the number of pixels to be filled.

Advantages

There are two primary technical requisites that favor the use of the painter’s algorithm.

Basic Graphical Structure

The painter’s algorithm is not as complex in structure as its other depth sorting algorithm counterparts.[9][11] Components such as the depth-based rendering order, as employed by the painter’s algorithm, are one of the simplest ways to designate the order of graphical production.[8] This simplicity makes it useful in basic computer graphics output scenarios where an unsophisticated render will need to be made with little struggle.[9]

Memory Efficiency

In the early 70s, when the painter’s algorithm was developed, physical memory was relatively small.[12] This required programs to manage memory as efficiently as possible to conduct large tasks without crashing. The painter’s algorithm prioritizes the efficient use of memory but at the expense of higher processing power since all parts of all images must be rendered.[9]

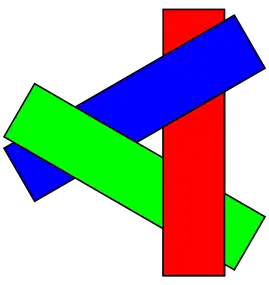
Overlapping polygons can cause the algorithm to fail

Limitations

The algorithm can fail in some cases, including cyclic overlap or piercing polygons.

Cyclical Overlapping

In the case of cyclic overlap, as shown in the figure to the right, Polygons A, B, and C overlap each other in such a way that it is impossible to determine which polygon is above the others. In this case, the offending polygons must be cut to allow sorting.[4]

Piercing Polygons

The case of piercing polygons arises when one polygon intersects another. Similar to cyclic overlap, this problem may be resolved by cutting the offending polygons.[4]

Efficiency

In basic implementations, the painter's algorithm can be inefficient. It forces the system to render each point on every polygon in the visible set, even if that polygon is occluded in the finished scene. This means that, for detailed scenes, the painter's algorithm can overly tax the computer hardware.

Variants

Extended painter's algorithm

Newell's algorithm, proposed as the extended algorithm to painter's algorithm, provides a method for cutting cyclical and piercing polygons.[4]

Reverse painter's algorithm

Another variant of painter's algorithm includes reverse painter's algorithm. Reverse painter's algorithm paints objects nearest to the viewer first — with the rule that paint must never be applied to parts of the image that are already painted (unless they are partially transparent). In a computer graphic system, this can be very efficient since it is not necessary to calculate the colors (using lighting, texturing, and such) for parts of a distant scene that are hidden by nearby objects. However, the reverse algorithm suffers from many of the same problems as the standard version.

Other computer graphics algorithms

The flaws of painter's algorithm led to the development of Z-buffer techniques, which can be viewed as a development of the painter's algorithm by resolving depth conflicts on a pixel-by-pixel basis, reducing the need for a depth-based rendering order.[13] Even in such systems, a variant of the painter's algorithm is sometimes employed. As Z-buffer implementations generally rely on fixed-precision depth-buffer registers implemented in hardware, there is scope for visibility problems due to rounding error. These are overlaps or gaps at joints between polygons. To avoid this, some graphics engine implementations "overrender", drawing the affected edges of both polygons in the order given by the painter's algorithm. This means that some pixels are actually drawn twice (as in the full painter's algorithm), but this happens on only small parts of the image and has a negligible performance effect.

References
  • Foley, James; Feiner, Steven K.; Hughes, John F. (1990). Computer Graphics: Principles and Practice. Reading, MA, USA: Addison-Wesley. p. 1174. ISBN 0-201-12110-7.
  1. Appel, Arthur (1968). Morrel, A. J. H. (ed.). "On calculating the illusion of reality" (PDF). Information Processing, Proceedings of IFIP Congress 1968, Edinburgh, UK, 5-10 August 1968, Volume 2 - Hardware, Applications: 945–950.
  2. Romney, Gordon Wilson (1969-09-01). "Computer Assisted Assembly and Rendering of Solids". Cite journal requires |journal= (help)
  3. Gary Scott Watkins. 1970. "A real time visible surface algorithm. Ph.D. Dissertation." The University of Utah. Order Number: AAI7023061.
  4. Newell, M. E.; Newell, R. G.; Sancha, T. L. (1972-08-01). "A solution to the hidden surface problem" (PDF). Proceedings of the ACM Annual Conference - Volume 1. ACM '72. Boston, Massachusetts, USA: Association for Computing Machinery. 1: 443–450. doi:10.1145/800193.569954. ISBN 978-1-4503-7491-0. S2CID 13829930.
  5. Bouknight, W. Jack (1970-09-01). "A procedure for generation of three-dimensional half-toned computer graphics presentations". Communications of the ACM. 13 (9): 527–536. doi:10.1145/362736.362739. ISSN 0001-0782. S2CID 15941472.
  6. Berland, Dinah (1995). Historical Painting Techniques, Materials, and Studio Practice. https://www.getty.edu/conservation/publications_resources/pdf_publications/pdf/historical_paintings.pdf: The Getty Conservation Institute.
  7. Wylie, Chris; Romney, Gordon; Evans, David; Erdahl, Alan (1967-11-14). "Half-tone perspective drawings by computer". Proceedings of the November 14–16, 1967, Fall Joint Computer Conference. AFIPS '67 (Fall). Anaheim, California: Association for Computing Machinery: 49–58. doi:10.1145/1465611.1465619. ISBN 978-1-4503-7896-3. S2CID 3282975.
  8. Desai, Apurva (2008). Computer Graphics. https://books.google.com/books?id=WQiIj8ZS0IoC&pg=PA256&lpg=PA256&dq=%22hewells%22+painter%27s+algorithm&source=bl&ots=HbWXoialNt&sig=ACfU3U0do0uKya5QGDaBUKKrXoYJ3uULdA&hl=en&sa=X&ved=2ahUKEwjh1tC14MHsAhUogK0KHWS5BsQQ6AEwAnoECAoQAg#v=onepage&q&f=false: PHI Learning Pvt. Ltd.CS1 maint: location (link)
  9. de Berg, Mark (2008). Computational Geometry. https://people.inf.elte.hu/fekete/algoritmusok_msc/terinfo_geom/konyvek/Computational%20Geometry%20-%20Algorithms%20and%20Applications,%203rd%20Ed.pdf: Springer.CS1 maint: location (link)
  10. de Berg, Mark (1993). Ray Shooting, Depth Orders and Hidden Surface Removal. Lecture Notes in Computer Science. 703. Springer. p. 130. ISBN 9783540570202{{inconsistent citations}}.
  11. Warnock, John E. (1969-06-01). "A Hidden Surface Algorithm for Computer Generated Halftone Pictures". Cite journal requires |journal= (help)
  12. Freiser, M.; Marcus, P. (June 1969). "A survey of some physical limitations on computer elements". IEEE Transactions on Magnetics. 5 (2): 82–90. Bibcode:1969ITM.....5...82F. doi:10.1109/TMAG.1969.1066403. ISSN 1941-0069.
  13. Nyberg, Daniel (2011). Analysis of Two Common Hidden Surface Removal Algorithms, Painter's Algorithm & Z-Buffering.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.