Plane partition

In mathematics and especially in combinatorics, a plane partition is a two-dimensional array of nonnegative integers ${\displaystyle \pi _{i,j}}$ (with positive integer indices i and j) that is nonincreasing in both indices. This means that

${\displaystyle \pi _{i,j}\geq \pi _{i,j+1}\quad }$ and ${\displaystyle \quad \pi _{i,j}\geq \pi _{i+1,j}\,}$ for all i and j.

A plane partition represented as piles of unit cubes

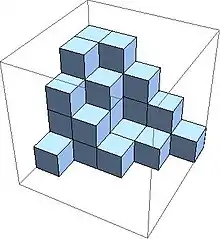
Moreover, only finitely many of the ${\displaystyle \pi _{i,j}}$ are nonzero. A plane partitions may be represented visually by the placement of a stack of ${\displaystyle \pi _{i,j}}$ unit cubes above the point (i, j) in the plane, giving a three-dimensional solid as shown in the picture.

The sum of a plane partition is

${\displaystyle n=\sum _{i,j}\pi _{i,j}.}$

The sum describes the number of cubes of which the plane partition consists. The number of plane partitions with sum n is denoted PL(n).

For example, there are six plane partitions with sum 3:

${\displaystyle {\begin{matrix}1&1&1\end{matrix}}\qquad {\begin{matrix}1&1\\1&\end{matrix}}\qquad {\begin{matrix}1\\1\\1&\end{matrix}}\qquad {\begin{matrix}2&1&\end{matrix}}\qquad {\begin{matrix}2\\1&\end{matrix}}\qquad {\begin{matrix}3\end{matrix}}}$

so PL(3) = 6. (Here the plane partitions are drawn using matrix indexing for the coordinates and the entries equal to 0 are suppressed for readability.) Let ${\displaystyle N_{i}(r,s,t)}$ be the total number of plane partitions in which r is the number of rows that are unequal to zero, s is the number of columns that are non-zero, and t is the largest integer of the matrix. Plane partitions are often described by the positions of the unit cubes. Therefore, a plane partition is defined as a finite subset ${\displaystyle {\mathcal {P}}}$ of positive integer lattice points (i, j, k) in ${\displaystyle \mathbb {N} ^{3}}$, such that if (r, s, t) lies in ${\displaystyle {\mathcal {P}}}$ and if (i, j, k) satisfies ${\displaystyle 1\leq i\leq r}$, ${\displaystyle 1\leq j\leq s}$ and ${\displaystyle 1\leq k\leq t}$, then (i, j, k) also lies in ${\displaystyle {\mathcal {P}}}$.

${\displaystyle {\mathcal {B}}(r,s,t)=\{(i,j,k)|1\leq i\leq r,1\leq j\leq s,1\leq k\leq t\}}$

Generating function of plane partitions

By a result of Percy A. MacMahon, the generating function for PL(n) is given by

${\displaystyle \sum _{n=0}^{\infty }\operatorname {PL} (n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{(1-x^{k})^{k}}}=1+x+3x^{2}+6x^{3}+13x^{4}+24x^{5}+\cdots .}$[1]

This is sometimes referred to as the MacMahon function.

This formula may be viewed as the 2-dimensional analogue of Euler's product formula for the number of integer partitions of n. There is no analogous formula known for partitions in higher dimensions (i.e., for solid partitions).[2] The asymptotics of plane partitions was worked out by E. M. Wright.[3] One obtains, for large ${\displaystyle n}$:

${\displaystyle \operatorname {PL} (n)\sim {\frac {\zeta (3)^{7/36}}{\sqrt {12\pi }}}\ \left({\frac {n}{2}}\right)^{-25/36}\ \exp \left(3\ \zeta (3)^{1/3}\left({\frac {n}{2}}\right)^{2/3}+\zeta '(-1)\right)\ ,}$

Here the typographical error (in Wright's paper) has been corrected, pointed out by Mutafchiev and Kamenov.[4] Evaluating numerically yields

${\displaystyle \ln \operatorname {PL} (n)\sim 2.00945n^{2/3}-0.69444\ln n-1.4631.}$

Around 1896 Percy A. MacMahon set up the generating function of plane partitions that are subsets of ${\displaystyle {\mathcal {B}}(r,s,t)}$ in his first paper on plane partitions.[5] The formula is given by

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,s,t)}q^{|\pi |}=\prod _{i=1}^{r}\prod _{j=1}^{s}{\frac {1-q^{i+j+t-1}}{1-q^{i+j-1}}}}$

A proof of this formula can be found in the book Combinatory Analysis written by Percy A. MacMahon.[6] Percy A. MacMahon also mentions in his book Combinatory Analysis the generating functions of plane partitions in article 429.[7] The formula for the generating function can be written in an alternative way, which is given by

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,s,t)}q^{|\pi |}=\prod _{i=1}^{r}\prod _{j=1}^{s}\prod _{k=1}^{t}{\frac {1-q^{i+j+k-1}}{1-q^{i+j+k-2}}}}$

Setting q = 1 in the formulas above yields

${\displaystyle N_{1}(r,s,t)=\prod _{(i,j,k)\in {\mathcal {B}}(r,s,t)}{\frac {i+j+k-1}{i+j+k-2}}=\prod _{i=1}^{r}\prod _{j=1}^{s}{\frac {i+j+t-1}{i+j-1}}}$

Percy A. MacMahon obtained that the total number of plane partitions in ${\displaystyle {\mathcal {B}}(r,s,t)}$ is given by ${\displaystyle N_{1}(r,s,t)}$.[8] The planar case (when t = 1) yields the binomial coefficients:

${\displaystyle {\mathcal {B}}(r,s,1)={\binom {r+s}{r}}}$

Ferrers diagrams for plane partitions

Another representation for plane partitions is in the form of Ferrers diagrams. The Ferrers diagram of a plane partition of ${\displaystyle n}$ is a collection of ${\displaystyle n}$ points or nodes, ${\displaystyle \lambda =(\mathbf {y} _{1},\mathbf {y} _{2},\ldots ,\mathbf {y} _{n})}$, with ${\displaystyle \mathbf {y} _{i}\in \mathbb {Z} _{\geq 0}^{3}}$ satisfying the condition:[9]

Condition FD: If the node ${\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})\in \lambda }$, then so do all the nodes ${\displaystyle \mathbf {y} =(y_{1},y_{2},y_{3})}$ with ${\displaystyle 0\leq y_{i}\leq a_{i}}$ for all ${\displaystyle i=1,2,3}$.

Replacing every node of a plane partition by a unit cube with edges aligned with the axes leads to the stack of cubes representation for the plane partition.

Equivalence of the two representations

Given a Ferrers diagram, one constructs the plane partition (as in the main definition) as follows.

Let ${\displaystyle \pi _{i,j}}$ be the number of nodes in the Ferrers diagram with coordinates of the form ${\displaystyle (i-1,j-1,*)}$ where ${\displaystyle *}$ denotes an arbitrary value. The collection ${\displaystyle \pi _{i,j}}$ form a plane partition. One can verify that condition FD implies that the conditions for a plane partition are satisfied.

Given a set of ${\displaystyle \pi _{i,j}}$ that form a plane partition, one obtains the corresponding Ferrers diagram as follows.

Start with the Ferrers diagram with no nodes. For every non-zero ${\displaystyle \pi _{i,j}}$, add ${\displaystyle \pi _{i,j}}$ nodes of the form ${\displaystyle (i-1,j-1,y_{3})}$ for ${\displaystyle 0\leq y_{3}<\pi _{i,j}-1}$ to the Ferrers diagram. By construction, it is easy to see that condition FD is satisfied.

For instance, below are shown the two representations of a plane partitions of 5.

${\displaystyle \left({\begin{smallmatrix}0\\0\\0\end{smallmatrix}}{\begin{smallmatrix}0\\0\\1\end{smallmatrix}}{\begin{smallmatrix}0\\1\\0\end{smallmatrix}}{\begin{smallmatrix}1\\0\\0\end{smallmatrix}}{\begin{smallmatrix}1\\1\\0\end{smallmatrix}}\right)\qquad \Longleftrightarrow \qquad {\begin{matrix}2&1\\1&1\end{matrix}}}$

Above, every node of the Ferrers diagram is written as a column and we have only written only the non-vanishing ${\displaystyle \pi _{i,j}}$ as is conventional.

Action of S₂, S₃ and C₃ on plane partitions

${\displaystyle {\mathcal {S}}_{2}}$ is the group of permutations acting on the first two coordinates of (i,j,k). This group contains the identity (i,j,k) and the transposition (i,j,k) → (j,i,k). The number of elements in an orbit ${\displaystyle \eta }$ is denoted by |${\displaystyle \eta }$|. ${\displaystyle {\mathcal {B}}/{\mathcal {S}}_{2}}$ denotes the set of orbits of elements of ${\displaystyle {\mathcal {B}}}$ under the action of ${\displaystyle {\mathcal {S}}_{2}}$. The height of an element (i,j,k) is defined by

${\displaystyle ht(i,j,k)=i+j+k-2}$

The height increases by one for each step away from the back right corner. For example, the corner position (1,1,1) has height 1 and ht(2,1,1)=2. ht(${\displaystyle \eta }$) is the height of an orbit, which is the height of any element in the orbit. This notation of the height differs from the notation of Ian G. Macdonald.[10]

There is a natural action of the permutation group ${\displaystyle {\mathcal {S}}_{3}}$ on a Ferrers diagram—this corresponds to simultaneously permuting the three coordinates of all nodes. This generalizes the conjugation operation for partitions. The action of ${\displaystyle {\mathcal {S}}_{3}}$ can generate new plane partitions starting from a given plane partition. Below there are shown six plane partitions of 4 that are generated by the ${\displaystyle {\mathcal {S}}_{3}}$ action. Only the exchange of the first two coordinates is manifest in the representation given below.

${\displaystyle {\begin{smallmatrix}3&1\end{smallmatrix}}\quad {\begin{smallmatrix}3\\1\end{smallmatrix}}\quad {\begin{smallmatrix}2&1&1\end{smallmatrix}}\quad {\begin{smallmatrix}2\\1\\1\end{smallmatrix}}\quad {\begin{smallmatrix}1&1&1\\1\end{smallmatrix}}\quad {\begin{smallmatrix}1&1\\1\\1\end{smallmatrix}}}$

${\displaystyle {\mathcal {C}}_{3}}$ is called the group of cyclic permutations and consists of

${\displaystyle (i,j,k)\rightarrow (i,j,k),\quad (i,j,k)\rightarrow (j,k,i),\quad {\text{and }}\quad (i,j,k)\rightarrow (k,i,j).}$

Symmetric plane partitions

A plane partition ${\displaystyle \pi }$ is called symmetric if π_i,j = π_j,i for all i,j . In other words, a plane partition is symmetric if (i,j,k)${\displaystyle \in {\mathcal {B}}(r,s,t)}$ if and only if (j,i,k)${\displaystyle \in {\mathcal {B}}(r,s,t)}$. Plane partitions of this type are symmetric with respect to the plane x = y. Below an example of a symmetric plane partition is given. Attached the matrix is visualised.

A symmetric plane partition with sum 35

${\displaystyle {\begin{matrix}4&3&3&2&1\\3&3&2&1&\\3&2&2&1&\\2&1&1&&\\1&&&&\end{matrix}}}$

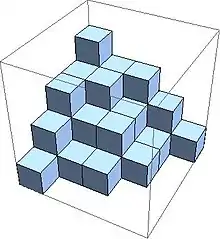
In 1898, Percy A. MacMahon formulated his conjecture about the generating function for symmetric plane partitions which are subsets of ${\displaystyle {\mathcal {B}}(r,r,t)}$.[11] This conjecture is called The MacMahon conjecture. The generating function is given by

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,r,t)/{\mathcal {S}}_{2}}q^{|\pi |}=\prod _{i=1}^{r}\left[{\frac {1-q^{t+2i-1}}{1-q^{2i-1}}}\prod _{j=i+1}^{r}{\frac {1-q^{2(i+j+t-1)}}{1-q^{2(i+j-1)}}}\right]}$

Ian G. Macdonald[10] pointed out that Percy A. MacMahon's conjecture reduces to

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,r,t)/{\mathcal {S}}_{2}}q^{|\pi |}=\prod _{\eta \in {\mathcal {B}}(r,r,t)/{\mathcal {S}}_{2}}{\frac {1-q^{|\eta |(1+ht(\eta ))}}{1-q^{|\eta |ht(\eta )}}}}$

In 1972 Edward A. Bender and Donald E. Knuth[12] conjectured a simple closed form for the generating function for plane partition which have at most r rows and strict decrease along the rows. George Andrews[13] showed, that the conjecture of Edward A. Bender and Donald E. Knuth and the MacMahon conjecture are equivalent. MacMahon's conjecture was proven almost simultaneously by George Andrews in 1977[14] and later Ian G. Macdonald presented an alternative proof[10] [example 16–19, pp. 83–86]. When setting q = 1 yields the counting function ${\displaystyle N_{2}(r,r,t)}$ which is given by

${\displaystyle N_{2}(r,r,t)=\prod _{i=1}^{r}{\frac {2i+t-1}{2i-1}}\prod _{1\leq i<j\leq r}{\frac {i+j+t-1}{i+j-1}}}$

For a proof of the case q = 1 please refer to George Andrews' paper MacMahon's conjecture on symmetric plane partitions.[15]

Cyclically symmetric plane partitions

π is called cyclically symmetric, if the i-th row of ${\displaystyle \pi }$ is conjugate to the i-th column for all i. The i-th row is regarded as an ordinary partition. The conjugate of a partition ${\displaystyle \pi }$ is the partition whose diagram is the transpose of partition ${\displaystyle \pi }$.[10] In other words, the plane partition is cyclically symmetric if whenever (i,j,k)${\displaystyle \in {\mathcal {B}}(r,s,t)}$ then (k,i,j) and (j,k,i) are as well in ${\displaystyle {\mathcal {B}}(r,s,t)}$. Below an example of a cyclically symmetric plane partition and its visualization is given.

A cyclically symmetric plane partition

${\displaystyle {\begin{matrix}6&5&5&4&3&3\\6&4&3&3&1&\\6&4&3&1&1&\\4&2&2&1&&\\3&1&1&&&\\1&1&1&&&\end{matrix}}}$

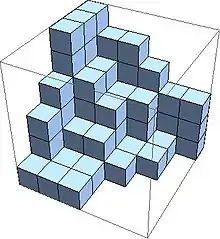
Ian G. Macdonald's conjecture provides a formula for calculating the number of cyclically symmetric plane partitions for a given integer r. This conjecture is called The Macdonald conjecture. The generating function for cyclically symmetric plane partitions which are subsets of ${\displaystyle {\mathcal {B}}(r,r,r)}$ is given by

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,r,r)/{\mathcal {C}}_{3}}q^{|\pi |}=\prod _{\eta \in {\mathcal {B}}(r,r,r)/{\mathcal {C}}_{3}}{\frac {1-q^{|\eta |(1+ht(\eta ))}}{1-q^{|\eta |ht(\eta )}}}}$

This equation can also be written in another way

${\displaystyle \prod _{\eta \in {\mathcal {B}}(r,r,r)/{\mathcal {C}}_{3}}{\frac {1-q^{|\eta |(1+ht(\eta ))}}{1-q^{|\eta |ht(\eta )}}}=\prod _{i=1}^{r}\left[{\frac {1-q^{3i-1}}{1-q^{3i-2}}}\prod _{j=i}^{r}{\frac {1-q^{3(r+i+j-1)}}{1-q^{3(2i+j-1)}}}\right]}$

In 1979 George Andrews has proven Macdonald's conjecture for the case q = 1 as the "weak" Macdonald conjecture.[16] Three years later William. H. Mills, David Robbins and Howard Rumsey proved the general case of Macdonald's conjecture in their paper Proof of the Macdonald conjecture.[17] The formula for ${\displaystyle N_{3}(r,r,r)}$ is given by the "weak" Macdonald conjecture

${\displaystyle N_{3}(r,r,r)=\prod _{i=1}^{r}\left[{\frac {3i-1}{3i-2}}\prod _{j=i}^{r}{\frac {i+j+r-1}{2i+j-1}}\right]}$

Totally symmetric plane partitions

A totally symmetric plane partition ${\displaystyle \pi }$ is a plane partition which is symmetric and cyclically symmetric. This means that the diagram is symmetric at all three diagonal planes. So therefore if (i,j,k)${\displaystyle \in {\mathcal {B}}(r,s,t)}$ then all six permutations of (i,j,k) are also in ${\displaystyle {\mathcal {B}}(r,s,t)}$. Below an example of a matrix for a totally symmetric plane partition is given. The picture shows the visualisation of the matrix.

A totally symmetric plane partition

${\displaystyle {\begin{matrix}5&4&4&3&1\\4&3&3&1&\\4&3&2&1&\\3&1&1&&\\1&&&&\end{matrix}}}$

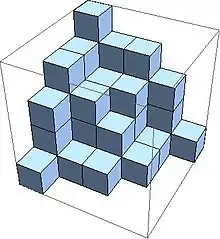
Ian G. Macdonald found the total number of totally symmetric plane partitions that are subsets of ${\displaystyle {\mathcal {B}}(r,r,r)}$. The formula is given by

${\displaystyle N_{4}(r,r,r)=\prod _{\eta \in {\mathcal {B}}(r,r,r)/{\mathcal {S}}_{3}}{\frac {1+ht(\eta )}{ht(\eta )}}}$

In 1995 John R. Stembridge first proved the formula for ${\displaystyle N_{4}(r,r,r)}$[18] and later in 2005 it was proven by George Andrews, Peter Paule, and Carsten Schneider.[19] Around 1983 George Andrews and David Robbins independently stated an explicit product formula for the orbit-counting generating function for totally symmetric plane partitions.[20][21] This formula already alluded to in George E. Andrews' paper Totally symmetric plane partitions which was published 1980.[22] The conjecture is called The q-TSPP conjecture and it is given by:

Let ${\displaystyle {\mathcal {S}}_{3}}$ be the symmetric group. The orbit counting function for totally symmetric plane partitions that fit inside ${\displaystyle {\mathcal {B}}(r,r,r)}$ is given by the formula

${\displaystyle \sum _{\pi \in {\mathcal {B}}(r,r,r)/{\mathcal {S}}_{3}}q^{|\pi |}=\prod _{\eta \in {\mathcal {B}}(r,r,r)/{\mathcal {S}}_{3}}{\frac {1-q^{1+ht(\eta )}}{1-q^{ht(\eta )}}}=\prod _{1\leq i\leq j\leq k\leq r}{\frac {1-q^{i+j+k-1}}{1-q^{i+j+k-2}}}.}$

This conjecture turned into a Theorem in 2011. For a proof of the q-TSPP conjecture please refer to the paper A proof of George Andrews' and David Robbins' q-TSPP conjecture by Christoph Koutschan, Manuel Kauers and Doron Zeilberger.[23]

Self-complementary plane partitions

If ${\displaystyle \pi _{i,j}+\pi _{r-i+1,s-j+1}=t}$ for all ${\displaystyle 1\leq i\leq r}$, ${\displaystyle 1\leq j\leq s}$, then the plane partition is called self-complementary. It is necessary that the product ${\displaystyle r\cdot s\cdot t}$ is even. Below an example of a self-complementary symmetric plane partition and its visualisation is given.

A self-complementary plane partition

${\displaystyle {\begin{matrix}4&4&3&2&1\\4&2&2&2&\\3&2&1&&\end{matrix}}}$

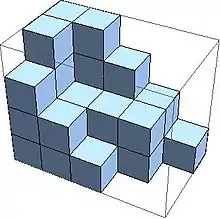
Richard P. Stanley[24] conjectured formulas for the total number of self-complementary plane partitions ${\displaystyle N_{5}(r,s,t)}$. According to Richard Stanley, David Robbins also formulated formulas for the total number of self-complementary plane partitions in a different but equivalent form. The total number of self-complementary plane partitions that are subsets of ${\displaystyle {\mathcal {B}}(r,s,t)}$ is given by

${\displaystyle N_{5}(2r,2s,2t)=N_{1}(r,s,t)^{2}}$

${\displaystyle N_{5}(2r+1,2s,2t)=N_{1}(r,s,t)N_{1}(r+1,s,t)}$

${\displaystyle N_{5}(2r+1,2s+1,2t)=N_{1}(r+1,s,t)N_{1}(r,s+1,t)}$

It is necessary that the product of r,s and t is even. A proof can be found in the paper Symmetries of Plane Partitions which was written by Richard P. Stanley.[25][24] The proof works with Schur functions ${\displaystyle s_{s^{r}}(x)}$. Stanley's proof of the ordinary enumeration of self-complementary plane partitions yields the q-analogue by substituting ${\displaystyle x_{i}=q^{i}}$ for ${\displaystyle i=1,\ldots ,n}$.[26] This is a special case of Stanley's hook-content formula.[27] The generating function for self-complementary plane partitions is given by

${\displaystyle s_{\gamma ^{\alpha }}(q,q^{2},\ldots ,q^{n})=q^{\gamma \alpha (\alpha +1)/2}\prod _{i=1}^{\alpha }\prod _{j=0}^{\gamma -1}{\frac {1-q^{i+n-\alpha +j}}{1-q^{i+j}}}}$

Substituting this formula in

${\displaystyle s_{s^{r}}(x_{1},x_{2},\ldots ,x_{t+r})^{2}\ {\text{ for }}{\mathcal {B}}(2r,2s,2t)}$

${\displaystyle s_{s^{r}}(x_{1},x_{2},\ldots ,x_{t+r})s_{(s+1)^{r}}(x_{1},x_{2},\ldots ,x_{t+r}){\text{ for }}{\mathcal {B}}(2r,2s+1,2t)}$

${\displaystyle s_{s^{r+1}}(x_{1},x_{2},\ldots ,x_{t+r+1})s_{s^{r}}(x_{1},x_{2},\ldots ,x_{t+r+1}){\text{ for }}{\mathcal {B}}(2r+1,2s,2t+1)}$

supplies the desired q-analogue case.

Cyclically symmetric self-complementary plane partitions

A plane partition ${\displaystyle \pi }$ is called cyclically symmetric self-complementary if it is cyclically symmetric and self-complementary. The figure presents a cyclically symmetric self-complementary plane partition and the according matrix is below.

A cyclically symmetric self-complementary plane partition

${\displaystyle {\begin{matrix}4&4&4&1\\3&3&2&1\\3&2&1&1\\3&&&\end{matrix}}}$

In a private communication with Richard P. Stanley, David Robbins conjectured that the total number of cyclically symmetric self-complementary plane partitions is given by ${\displaystyle N_{6}(2r,2r,2r)}$.[21][24] The total number of cyclically symmetric self-complementary plane partitions is given by

${\displaystyle N_{6}(2r,2r,2r)=D_{r}^{2}}$

${\displaystyle D_{r}}$ is the number of ${\displaystyle r\times r}$ alternating sign matrices. A formula for ${\displaystyle D_{r}}$ is given by

${\displaystyle D_{r}=\prod _{j=0}^{r-1}{\frac {(3j+1)!}{(r+j)!}}}$

Greg Kuperberg proved the formula for ${\displaystyle N_{6}(r,r,r)}$ in 1994.[28]

Totally symmetric self-complementary plane partitions

A totally symmetric self-complementary plane partition is a plane partition that is both totally symmetric and self-complementary. For instance, the matrix below is such a plane partition; it is visualised in the accompanying picture.

A totally symmetric self-complementary plane partition

${\displaystyle {\begin{matrix}6&6&6&5&5&3\\6&5&5&3&3&1\\6&5&5&3&3&1\\5&3&3&1&1&\\5&3&3&1&1&\\3&1&1&&&\end{matrix}}}$

The formula ${\displaystyle N_{7}(r,r,r)}$ was conjectured by William H. Mills, David Robbins and Howard Rumsey in their work Self-Complementary Totally Symmetric Plane Partitions.[29] The total number of totally symmetric self-complementary plane partitions is given by

${\displaystyle N_{7}(2r,2r,2r)=D_{r}}$

George Andrews has proven this formula in 1994 in his paper Plane Partitions V: The TSSCPP Conjecture.[30]

References

1. Richard P. Stanley, Enumerative Combinatorics, Volume 2. Corollary 7.20.3.
2. R.P. Stanley, Enumerative Combinatorics, Volume 2. pp. 365, 401–2.
3. E. M. Wright, Asymptotic partition formulae I. Plane partitions, The Quarterly Journal of Mathematics 1 (1931) 177–189.
4. L. Mutafchiev and E. Kamenov, "Asymptotic formula for the number of plane partitions of positive integers", Comptus Rendus-Academie Bulgare Des Sciences 59 (2006), no. 4, 361.
5. MacMahon, Percy A. (1896). "XVI. Memoir on the theory of the partition of numbers.-Part I". Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 187: Article 52.
6. MacMahon, Major Percy A. (1916). Combinatory Analysis Vol 2. Cambridge University Press. pp. §495.
7. MacMahon, Major Percy A. (1916). Combinatory Analysis. 2. Cambridge University Press. pp. §429.
8. MacMahon, Major Percy A. (1916). Combinatory Analysis. Cambridge University Press. pp. §429, §494.
9. Atkin, A. O. L.; Bratley, P.; Macdonald, I. G.; McKay, J. K. S. (1967). "Some computations for m-dimensional partitions". Proc. Camb. Phil. Soc. 63 (4): 1097–1100. Bibcode:1967PCPS...63.1097A. doi:10.1017/s0305004100042171.
10. Macdonald, Ian G. (1998). Symmetric Functions and Hall Polynomials. Clarendon Press. pp. 20f, 85f. ISBN 9780198504504.
11. MacMahon, Percy Alexander (1899). "Partitions of numbers whose graphs possess symmetry". Transactions of the Cambridge Philosophical Society. 17.
12. Bender & Knuth (1972). "Enumeration of plane partitions". Journal of Combinatorial Theory, Series A. 13: 40–54. doi:10.1016/0097-3165(72)90007-6.
13. Andrews, George E. (1977). "Plane partitions II: The equivalence of the Bender-Knuth and MacMahon conjectures". Pacific Journal of Mathematics. 72 (2): 283–291. doi:10.2140/pjm.1977.72.283.
14. Andrews, George (1975). "Plane Partitions (I): The Mac Mahon Conjecture". Adv. Math. Suppl. Stud. 1.
15. Andrews, George E. (1977). "MacMahon's conjecture on symmetric plane partitions". Proceedings of the National Academy of Sciences. 74 (2): 426–429. Bibcode:1977PNAS...74..426A. doi:10.1073/pnas.74.2.426. PMC 392301. PMID 16592386.
16. Andrews, George E. (1979). "Plane Partitions(III): The Weak Macdonald Conjecture". Inventiones Mathematicae. 53 (3): 193–225. Bibcode:1979InMat..53..193A. doi:10.1007/bf01389763. S2CID 122528418.
17. Mills; Robbins; Rumsey (1982). "Proof of the Macdonald conjecture". Inventiones Mathematicae. 66: 73–88. Bibcode:1982InMat..66...73M. doi:10.1007/bf01404757. S2CID 120926391.
18. Stembridge, John R. (1995). "The Enumeration of Totally Symmetric Plane Partitions". Advances in Mathematics. 111 (2): 227–243. doi:10.1006/aima.1995.1023.
19. Andrews; Paule; Schneider (2005). "Plane Partitions VI: Stembridge's TSPP theorem". Advances in Applied Mathematics. 34 (4): 709–739. doi:10.1016/j.aam.2004.07.008.
20. Bressoud, David M. (1999). Proofs and Confirmations. Cambridge University Press. pp. conj. 13. ISBN 9781316582756.
21. Stanley, Richard P. (1970). "A Baker's dozen of conjectures concerning plane partitions". Combinatoire énumérative: 285–293.
22. Andrews, George (1980). "Totally symmetric plane partitions". Abstracts Amer. Math. Soc. 1: 415.
23. Koutschan; Kauers; Zeilberger (2011). "A proof of George Andrews' and David Robbins' q-TSPP conjecture". PNAS. 108 (6): 2196–2199. arXiv:1002.4384. Bibcode:2011PNAS..108.2196K. doi:10.1073/pnas.1019186108. S2CID 12077490.
24. Stanley, Richard P. (1986). "Symmetries of Plane Partitions". Journal of Combinatorial Theory, Series A. 43: 103–113. doi:10.1016/0097-3165(86)90028-2.
25. "Erratum". Journal of Combinatorial Theory. 43: 310. 1986.
26. Eisenkölbl, Theresia (2008). "A Schur function identity related to the (−1)-enumeration of self complementary plane partitions". Journal of Combinatorial Theory, Series A. 115: 199–212. doi:10.1016/j.jcta.2007.05.004.
27. Stanley, Richard P. (1971). "Theory and Application of Plane Partitions. Part 2". Advances in Applied Mathematics. 50 (3): 259–279. doi:10.1002/sapm1971503259.
28. Kuperberg, Greg (1994). "Symmetries of plane partitions and the permanent-determinant method". Journal of Combinatorial Theory, Series A. 68: 115–151. arXiv:math/9410224. Bibcode:1994math.....10224K. doi:10.1016/0097-3165(94)90094-9. S2CID 14538036.
29. Mills; Robbins; Rumsey (1986). "Self-Complementary Totally Symmetric Plane Partitions". Journal of Combinatorial Theory, Series A. 42 (2): 277–292. doi:10.1016/0097-3165(86)90098-1.
30. Andrews, George E. (1994). "Plane Partitions V: The TSSCPP Conjecture". Journal of Combinatorial Theory, Series A. 66: 28–39. doi:10.1016/0097-3165(94)90048-5.

• G. Andrews, The Theory of Partitions, Cambridge University Press, Cambridge, 1998, ISBN 0-521-63766-X
• Bender, Edward A.; Knuth, Donald E. (1972), "Enumeration of plane partitions", Journal of Combinatorial Theory, Series A, 13: 40–54, doi:10.1016/0097-3165(72)90007-6, ISSN 1096-0899, MR 0299574
• I.G. Macdonald, Symmetric Functions and Hall Polynomials, Oxford University Press, Oxford, 1999, ISBN 0-19-850450-0
• P.A. MacMahon, Combinatory analysis, 2 vols, Cambridge University Press, 1915–16.

External links

• Weisstein, Eric W. "Plane partition". MathWorld.
• OEIS sequence A000219 (Number of planar partitions of n)
• The DLMF page on Plane Partitions