Quadruplanar-Inversor

The Quadruplanar inversor of Sylvester and Kempe is a generalization of Hart's inversor. Like Hart's inversor, is a mechanism that provides a perfect straight line motion without sliding guides.

The mechanism was described in 1875 by James Joseph Sylvester in the journal Nature.[1]

Like Hart's inversor, it is based on an antiparallelogram (KBCD in the figures below) but the rather than placing the fixed, input and output points on the sides (dividing them in fixed proportion so they are all similar), Sylvester recognized that the additional points could be displaced sideways off the sides, as long as they formed similar triangles. Hart's original form is simply the degenerate case of triangles with altitude zero.

In these diagrams:

  • KBCD is an antiparallelogram, so KB = CD and BC = DK.
  • KBA, CBB0, and CDE (and KDI in the first diagram) are similar triangles.
    • Because KB = CD, KBA and CDE are congruent triangles
    • Because BC = DK, CBB0 and KDI are congruent triangles
  • A0 and B0 are fixed points.
  • A0A = A0B0, i.e. A moves on a circle through B.
  • E moves in a straight line
  • Example 1
  • Animation
  • Graphic
  • Description
  • Example 2
  • Animation
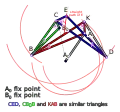  • Graphic
  • Example 3
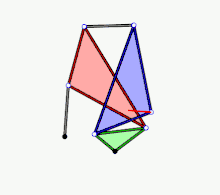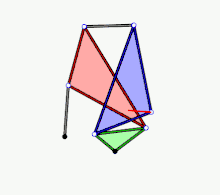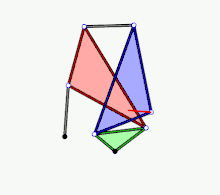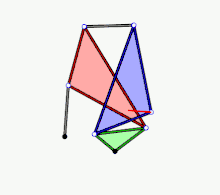  • Animation
  • Graphic
  • Description

References
  1. Sylvester, J.J. (15 July 1875). "History of the Plagiograph". Nature. XII (298): 214–216. Bibcode:1875Natur..12..214S. doi:10.1038/012214b0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.