Rainbow

A rainbow is a meteorological phenomenon that is caused by reflection, refraction and dispersion of light in water droplets resulting in a spectrum of light appearing in the sky. It takes the form of a multicoloured circular arc. Rainbows caused by sunlight always appear in the section of sky directly opposite the sun.

For other uses, see Rainbow (disambiguation).

Double rainbow and supernumerary rainbows on the inside of the primary arc. The shadow of the photographer's head on the bottom marks the centre of the rainbow circle (antisolar point).

Rainbows can be full circles. However, the observer normally sees only an arc formed by illuminated droplets above the ground,[1] and centered on a line from the sun to the observer's eye.

In a primary rainbow, the arc shows red on the outer part and violet on the inner side. This rainbow is caused by light being refracted when entering a droplet of water, then reflected inside on the back of the droplet and refracted again when leaving it.

In a double rainbow, a second arc is seen outside the primary arc, and has the order of its colours reversed, with red on the inner side of the arc. This is caused by the light being reflected twice on the inside of the droplet before leaving it.

Overview
Image of the end of a rainbow at Jasper National Park

A rainbow is not located at a specific distance from the observer, but comes from an optical illusion caused by any water droplets viewed from a certain angle relative to a light source. Thus, a rainbow is not an object and cannot be physically approached. Indeed, it is impossible for an observer to see a rainbow from water droplets at any angle other than the customary one of 42 degrees from the direction opposite the light source. Even if an observer sees another observer who seems "under" or "at the end of" a rainbow, the second observer will see a different rainbow—farther off—at the same angle as seen by the first observer.

Rainbows span a continuous spectrum of colours. Any distinct bands perceived are an artefact of human colour vision, and no banding of any type is seen in a black-and-white photo of a rainbow, only a smooth gradation of intensity to a maximum, then fading towards the other side. For colours seen by the human eye, the most commonly cited and remembered sequence is Isaac Newton's sevenfold red, orange, yellow, green, blue, indigo and violet,[2][lower-alpha 1] remembered by the mnemonic Richard Of York Gave Battle In Vain (ROYGBIV).

Rainbows can be caused by many forms of airborne water. These include not only rain, but also mist, spray, and airborne dew.

Visibility
Rainbows can form in the spray of a waterfall (called spray bows)
A mistbow over Rannoch Moor in Scotland
Rainbows may form in the spray created by waves

Rainbows can be observed whenever there are water drops in the air and sunlight shining from behind the observer at a low altitude angle. Because of this, rainbows are usually seen in the western sky during the morning and in the eastern sky during the early evening. The most spectacular rainbow displays happen when half the sky is still dark with raining clouds and the observer is at a spot with clear sky in the direction of the sun. The result is a luminous rainbow that contrasts with the darkened background. During such good visibility conditions, the larger but fainter secondary rainbow is often visible. It appears about 10° outside of the primary rainbow, with inverse order of colours.

Eruption of Castle Geyser, Yellowstone National Park, with double rainbow seen in the mist

The rainbow effect is also commonly seen near waterfalls or fountains. In addition, the effect can be artificially created by dispersing water droplets into the air during a sunny day. Rarely, a moonbow, lunar rainbow or nighttime rainbow, can be seen on strongly moonlit nights. As human visual perception for colour is poor in low light, moonbows are often perceived to be white.[4]

It is difficult to photograph the complete semicircle of a rainbow in one frame, as this would require an angle of view of 84°. For a 35 mm camera, a wide-angle lens with a focal length of 19 mm or less would be required. Now that software for stitching several images into a panorama is available, images of the entire arc and even secondary arcs can be created fairly easily from a series of overlapping frames.

From above the earth such as in an aeroplane, it is sometimes possible to see a rainbow as a full circle. This phenomenon can be confused with the glory phenomenon, but a glory is usually much smaller, covering only 5–20°.

The sky inside a primary rainbow is brighter than the sky outside of the bow. This is because each raindrop is a sphere and it scatters light over an entire circular disc in the sky. The radius of the disc depends on the wavelength of light, with red light being scattered over a larger angle than blue light. Over most of the disc, scattered light at all wavelengths overlaps, resulting in white light which brightens the sky. At the edge, the wavelength dependence of the scattering gives rise to the rainbow.[5]

Light of primary rainbow arc is 96% polarised tangential to the arch.[6] Light of second arc is 90% polarised.

Number of colours in a spectrum or a rainbow

A spectrum obtained using a glass prism and a point source is a continuum of wavelengths without bands. The number of colours that the human eye is able to distinguish in a spectrum is in the order of 100.[7] Accordingly, the Munsell colour system (a 20th-century system for numerically describing colours, based on equal steps for human visual perception) distinguishes 100 hues. The apparent discreteness of main colours is an artefact of human perception and the exact number of main colours is a somewhat arbitrary choice.

Newton, who admitted his eyes were not very critical in distinguishing colours,[8] originally (1672) divided the spectrum into five main colours: red, yellow, green, blue and violet. Later he included orange and indigo, giving seven main colours by analogy to the number of notes in a musical scale.[2][lower-alpha 2][9] Newton chose to divide the visible spectrum into seven colours out of a belief derived from the beliefs of the ancient Greek sophists, who thought there was a connection between the colours, the musical notes, the known objects in the Solar System, and the days of the week.[10][11][12] Scholars have noted that what Newton regarded at the time as "blue" would today be regarded as cyan, and what Newton called "indigo" would today be considered blue.[3]

Rainbow (middle: real, bottom: computed) compared to true spectrum (top): unsaturated colours and different colour profile
Newton's first colours Red Yellow Green Blue Violet
Newton's later colours Red Orange Yellow Green Blue Indigo Violet
Modern colours Red Orange Yellow Green Cyan Blue Violet

The colour pattern of a rainbow is different from a spectrum, and the colours are less saturated. There is spectral smearing in a rainbow owing to the fact that for any particular wavelength, there is a distribution of exit angles, rather than a single unvarying angle.[13] In addition, a rainbow is a blurred version of the bow obtained from a point source, because the disk diameter of the sun (0.5°) cannot be neglected compared to the width of a rainbow (2°). Further red of the first supplementary rainbow overlaps the violet of the primary rainbow, so rather than the final colour being a variant of spectral violet, it is actually a purple. The number of colour bands of a rainbow may therefore be different from the number of bands in a spectrum, especially if the droplets are particularly large or small. Therefore, the number of colours of a rainbow is variable. If, however, the word rainbow is used inaccurately to mean spectrum, it is the number of main colours in the spectrum.

The question of whether everyone sees seven colours in a rainbow is related to the idea of linguistic relativity. Suggestions have been made that there is universality in the way that a rainbow is perceived.[14][15] However, more recent research suggests that the number of distinct colours observed and what these are called depend on the language that one uses, with people whose language has fewer colour words seeing fewer discrete colour bands.[16]

Explanation
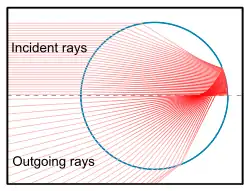
Light rays enter a raindrop from one direction (typically a straight line from the sun), reflect off the back of the raindrop, and fan out as they leave the raindrop. The light leaving the rainbow is spread over a wide angle, with a maximum intensity at the angles 40.89–42°. (Note: Between 2 and 100% of the light is reflected at each of the three surfaces encountered, depending on the angle of incidence. This diagram only shows the paths relevant to the rainbow.)
White light separates into different colours on entering the raindrop due to dispersion, causing red light to be refracted less than blue light.

When sunlight encounters a raindrop, part of the light is reflected and the rest enters the raindrop. The light is refracted at the surface of the raindrop. When this light hits the back of the raindrop, some of it is reflected off the back. When the internally reflected light reaches the surface again, once more some is internally reflected and some is refracted as it exits the drop. (The light that reflects off the drop, exits from the back, or continues to bounce around inside the drop after the second encounter with the surface, is not relevant to the formation of the primary rainbow.) The overall effect is that part of the incoming light is reflected back over the range of 0° to 42°, with the most intense light at 42°.[17] This angle is independent of the size of the drop, but does depend on its refractive index. Seawater has a higher refractive index than rain water, so the radius of a "rainbow" in sea spray is smaller than a true rainbow. This is visible to the naked eye by a misalignment of these bows.[18]

The reason the returning light is most intense at about 42° is that this is a turning point – light hitting the outermost ring of the drop gets returned at less than 42°, as does the light hitting the drop nearer to its centre. There is a circular band of light that all gets returned right around 42°. If the sun were a laser emitting parallel, monochromatic rays, then the luminance (brightness) of the bow would tend toward infinity at this angle (ignoring interference effects). (See Caustic (optics).) But since the sun's luminance is finite and its rays are not all parallel (it covers about half a degree of the sky) the luminance does not go to infinity. Furthermore, the amount by which light is refracted depends upon its wavelength, and hence its colour. This effect is called dispersion. Blue light (shorter wavelength) is refracted at a greater angle than red light, but due to the reflection of light rays from the back of the droplet, the blue light emerges from the droplet at a smaller angle to the original incident white light ray than the red light. Due to this angle, blue is seen on the inside of the arc of the primary rainbow, and red on the outside. The result of this is not only to give different colours to different parts of the rainbow, but also to diminish the brightness. (A "rainbow" formed by droplets of a liquid with no dispersion would be white, but brighter than a normal rainbow.)

The light at the back of the raindrop does not undergo total internal reflection, and some light does emerge from the back. However, light coming out the back of the raindrop does not create a rainbow between the observer and the sun because spectra emitted from the back of the raindrop do not have a maximum of intensity, as the other visible rainbows do, and thus the colours blend together rather than forming a rainbow.[19]

A rainbow does not exist at one particular location. Many rainbows exist; however, only one can be seen depending on the particular observer's viewpoint as droplets of light illuminated by the sun. All raindrops refract and reflect the sunlight in the same way, but only the light from some raindrops reaches the observer's eye. This light is what constitutes the rainbow for that observer. The whole system composed by the sun's rays, the observer's head, and the (spherical) water drops has an axial symmetry around the axis through the observer's head and parallel to the sun's rays. The rainbow is curved because the set of all the raindrops that have the right angle between the observer, the drop, and the sun, lie on a cone pointing at the sun with the observer at the tip. The base of the cone forms a circle at an angle of 40–42° to the line between the observer's head and their shadow but 50% or more of the circle is below the horizon, unless the observer is sufficiently far above the earth's surface to see it all, for example in an aeroplane (see above).[20][21] Alternatively, an observer with the right vantage point may see the full circle in a fountain or waterfall spray.[22]

Mathematical derivation
Mathematical derivation

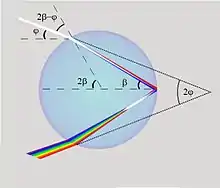
It is possible to determine the perceived angle which the rainbow subtends as follows.[23]

Given a spherical raindrop, and defining the perceived angle of the rainbow as 2φ, and the angle of the internal reflection as 2β, then the angle of incidence of the sun's rays with respect to the drop's surface normal is 2β − φ. Since the angle of refraction is β, Snell's law gives us

sin(2β − φ) = n sin β,

where n = 1.333 is the refractive index of water. Solving for φ, we get

φ = 2β − arcsin(n sin β).

The rainbow will occur where the angle φ is maximum with respect to the angle β. Therefore, from calculus, we can set dφ/dβ = 0, and solve for β, which yields

.

Substituting back into the earlier equation for φ yields 2φmax ≈ 42° as the radius angle of the rainbow.

Variations

Double rainbows
"Double rainbow" redirects here. For other uses, see Double Rainbow.
Double rainbow with Alexander's band visible between the primary and secondary bows. Also note the pronounced supernumerary bows inside the primary bow.
Physics of a primary and secondary rainbow and Alexander's dark band[24] (The image of the sun in the picture is only conventional; all rays are parallel to the axis of the rainbow's cone)

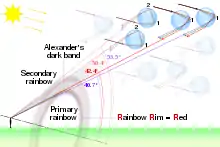
A secondary rainbow, at a greater angle than the primary rainbow, is often visible. The term double rainbow is used when both the primary and secondary rainbows are visible. In theory, all rainbows are double rainbows, but since the secondary bow is always fainter than the primary, it may be too weak to spot in practice.

Secondary rainbows are caused by a double reflection of sunlight inside the water droplets. Technically the secondary bow is centred on the sun itself, but since its angular size is more than 90° (about 127° for violet to 130° for red), it is seen on the same side of the sky as the primary rainbow, about 10° outside it at an apparent angle of 50–53°. As a result of the "inside" of the secondary bow being "up" to the observer, the colours appear reversed compared to those of the primary bow.

The secondary rainbow is fainter than the primary because more light escapes from two reflections compared to one and because the rainbow itself is spread over a greater area of the sky. Each rainbow reflects white light inside its coloured bands, but that is "down" for the primary and "up" for the secondary.[25] The dark area of unlit sky lying between the primary and secondary bows is called Alexander's band, after Alexander of Aphrodisias who first described it.[26]

Twinned rainbow

Unlike a double rainbow that consists of two separate and concentric rainbow arcs, the very rare twinned rainbow appears as two rainbow arcs that split from a single base.[27] The colours in the second bow, rather than reversing as in a secondary rainbow, appear in the same order as the primary rainbow. A "normal" secondary rainbow may be present as well. Twinned rainbows can look similar to, but should not be confused with supernumerary bands. The two phenomena may be told apart by their difference in colour profile: supernumerary bands consist of subdued pastel hues (mainly pink, purple and green), while the twinned rainbow shows the same spectrum as a regular rainbow. The cause of a twinned rainbow is the combination of different sizes of water drops falling from the sky. Due to air resistance, raindrops flatten as they fall, and flattening is more prominent in larger water drops. When two rain showers with different-sized raindrops combine, they each produce slightly different rainbows which may combine and form a twinned rainbow.[28] A numerical ray tracing study showed that a twinned rainbow on a photo could be explained by a mixture of 0.40 and 0.45 mm droplets. That small difference in droplet size resulted in a small difference in flattening of the droplet shape, and a large difference in flattening of the rainbow top.[29]

Circular rainbow

Meanwhile, the even rarer case of a rainbow split into three branches was observed and photographed in nature.[30]

Full-circle rainbow

In theory, every rainbow is a circle, but from the ground, usually only its upper half can be seen. Since the rainbow's centre is diametrically opposed to the sun's position in the sky, more of the circle comes into view as the sun approaches the horizon, meaning that the largest section of the circle normally seen is about 50% during sunset or sunrise. Viewing the rainbow's lower half requires the presence of water droplets below the observer's horizon, as well as sunlight that is able to reach them. These requirements are not usually met when the viewer is at ground level, either because droplets are absent in the required position, or because the sunlight is obstructed by the landscape behind the observer. From a high viewpoint such as a high building or an aircraft, however, the requirements can be met and the full-circle rainbow can be seen.[31][32] Like a partial rainbow, the circular rainbow can have a secondary bow or supernumerary bows as well.[33] It is possible to produce the full circle when standing on the ground, for example by spraying a water mist from a garden hose while facing away from the sun.[34]

A circular rainbow should not be confused with the glory, which is much smaller in diameter and is created by different optical processes. In the right circumstances, a glory and a (circular) rainbow or fog bow can occur together. Another atmospheric phenomenon that may be mistaken for a "circular rainbow" is the 22° halo, which is caused by ice crystals rather than liquid water droplets, and is located around the sun (or moon), not opposite it.

Supernumerary rainbows
High dynamic range photograph of a rainbow with additional supernumerary bands inside the primary bow

In certain circumstances, one or several narrow, faintly coloured bands can be seen bordering the violet edge of a rainbow; i.e., inside the primary bow or, much more rarely, outside the secondary. These extra bands are called supernumerary rainbows or supernumerary bands; together with the rainbow itself the phenomenon is also known as a stacker rainbow. The supernumerary bows are slightly detached from the main bow, become successively fainter along with their distance from it, and have pastel colours (consisting mainly of pink, purple and green hues) rather than the usual spectrum pattern.[35] The effect becomes apparent when water droplets are involved that have a diameter of about 1 mm or less; the smaller the droplets are, the broader the supernumerary bands become, and the less saturated their colours.[36] Due to their origin in small droplets, supernumerary bands tend to be particularly prominent in fogbows.[37]

Supernumerary rainbows cannot be explained using classical geometric optics. The alternating faint bands are caused by interference between rays of light following slightly different paths with slightly varying lengths within the raindrops. Some rays are in phase, reinforcing each other through constructive interference, creating a bright band; others are out of phase by up to half a wavelength, cancelling each other out through destructive interference, and creating a gap. Given the different angles of refraction for rays of different colours, the patterns of interference are slightly different for rays of different colours, so each bright band is differentiated in colour, creating a miniature rainbow. Supernumerary rainbows are clearest when raindrops are small and of uniform size. The very existence of supernumerary rainbows was historically a first indication of the wave nature of light, and the first explanation was provided by Thomas Young in 1804.[38]

Reflected rainbow, reflection rainbow

Reflected rainbow
Reflection rainbow (top) and normal rainbow (bottom) at sunset

When a rainbow appears above a body of water, two complementary mirror bows may be seen below and above the horizon, originating from different light paths. Their names are slightly different.

A reflected rainbow may appear in the water surface below the horizon.[39] The sunlight is first deflected by the raindrops, and then reflected off the body of water, before reaching the observer. The reflected rainbow is frequently visible, at least partially, even in small puddles.

A reflection rainbow may be produced where sunlight reflects off a body of water before reaching the raindrops, if the water body is large, quiet over its entire surface, and close to the rain curtain. The reflection rainbow appears above the horizon. It intersects the normal rainbow at the horizon, and its arc reaches higher in the sky, with its centre as high above the horizon as the normal rainbow's centre is below it. Reflection bows are usually brightest when the sun is low because at that time its light is most strongly reflected from water surfaces. As the sun gets lower the normal and reflection bows are drawn closer together. Due to the combination of requirements, a reflection rainbow is rarely visible.

Up to eight separate bows may be distinguished if the reflected and reflection rainbows happen to occur simultaneously: The normal (non-reflection) primary and secondary bows above the horizon (1, 2) with their reflected counterparts below it (3, 4), and the reflection primary and secondary bows above the horizon (5, 6) with their reflected counterparts below it (7, 8).[40][41]

Monochrome rainbow
Main article: Monochrome rainbow
Unenhanced photo of a red (monochrome) rainbow

Occasionally a shower may happen at sunrise or sunset, where the shorter wavelengths like blue and green have been scattered and essentially removed from the spectrum. Further scattering may occur due to the rain, and the result can be the rare and dramatic monochrome or red rainbow.[42]

Higher-order rainbows

In addition to the common primary and secondary rainbows, it is also possible for rainbows of higher orders to form. The order of a rainbow is determined by the number of light reflections inside the water droplets that create it: One reflection results in the first-order or primary rainbow; two reflections create the second-order or secondary rainbow. More internal reflections cause bows of higher orders—theoretically unto infinity.[43] As more and more light is lost with each internal reflection, however, each subsequent bow becomes progressively dimmer and therefore increasingly difficult to spot. An additional challenge in observing the third-order (or tertiary) and fourth-order (quaternary) rainbows is their location in the direction of the sun (about 40° and 45° from the sun, respectively), causing them to become drowned in its glare.[44]

For these reasons, naturally occurring rainbows of an order higher than 2 are rarely visible to the naked eye. Nevertheless, sightings of the third-order bow in nature have been reported, and in 2011 it was photographed definitively for the first time.[45][46] Shortly after, the fourth-order rainbow was photographed as well,[47][48] and in 2014 the first ever pictures of the fifth-order (or quinary) rainbow, located in between the primary and secondary bows, were published.[49] In a laboratory setting, it is possible to create bows of much higher orders. Felix Billet (1808–1882) depicted angular positions up to the 19th-order rainbow, a pattern he called a "rose of rainbows".[50][51][52] In the laboratory, it is possible to observe higher-order rainbows by using extremely bright and well collimated light produced by lasers. Up to the 200th-order rainbow was reported by Ng et al. in 1998 using a similar method but an argon ion laser beam.[53]

Tertiary and quaternary rainbows should not be confused with "triple" and "quadruple" rainbows—terms sometimes erroneously used to refer to the—much more common—supernumerary bows and reflection rainbows.

Rainbows under moonlight
Main article: Moonbow
Spray moonbow at the Lower Yosemite Fall

Like most atmospheric optical phenomena, rainbows can be caused by light from the Sun, but also from the Moon. In case of the latter, the rainbow is referred to as a lunar rainbow or moonbow. They are much dimmer and rarer than solar rainbows, requiring the Moon to be near-full in order for them to be seen. For the same reason, moonbows are often perceived as white and may be thought of as monochrome. The full spectrum is present, however, but the human eye is not normally sensitive enough to see the colours. Long exposure photographs will sometimes show the colour in this type of rainbow.[54]

Fogbow
Main article: Fog bow
Fogbow and glory.

Fogbows form in the same way as rainbows, but they are formed by much smaller cloud and fog droplets that diffract light extensively. They are almost white with faint reds on the outside and blues inside; often one or more broad supernumerary bands can be discerned inside the inner edge. The colours are dim because the bow in each colour is very broad and the colours overlap. Fogbows are commonly seen over water when air in contact with the cooler water is chilled, but they can be found anywhere if the fog is thin enough for the sun to shine through and the sun is fairly bright. They are very large—almost as big as a rainbow and much broader. They sometimes appear with a glory at the bow's centre.[55]

Fog bows should not be confused with ice halos, which are very common around the world and visible much more often than rainbows (of any order),[56] yet are unrelated to rainbows.

Circumhorizontal and circumzenithal arcs
A circumhorizontal arc (bottom), below a circumscribed halo
Circumzenithal arc

The circumzenithal and circumhorizontal arcs are two related optical phenomena similar in appearance to a rainbow, but unlike the latter, their origin lies in light refraction through hexagonal ice crystals rather than liquid water droplets. This means that they are not rainbows, but members of the large family of halos.

Both arcs are brightly coloured ring segments centred on the zenith, but in different positions in the sky: The circumzenithal arc is notably curved and located high above the Sun (or Moon) with its convex side pointing downwards (creating the impression of an "upside down rainbow"); the circumhorizontal arc runs much closer to the horizon, is more straight and located at a significant distance below the Sun (or Moon). Both arcs have their red side pointing towards the sun and their violet part away from it, meaning the circumzenithal arc is red on the bottom, while the circumhorizontal arc is red on top.[57][58]

The circumhorizontal arc is sometimes referred to by the misnomer "fire rainbow". In order to view it, the Sun or Moon must be at least 58° above the horizon, making it a rare occurrence at higher latitudes. The circumzenithal arc, visible only at a solar or lunar elevation of less than 32°, is much more common, but often missed since it occurs almost directly overhead.

Rainbows on Titan

It has been suggested that rainbows might exist on Saturn's moon Titan, as it has a wet surface and humid clouds. The radius of a Titan rainbow would be about 49° instead of 42°, because the fluid in that cold environment is methane instead of water. Although visible rainbows may be rare due to Titan's hazy skies, infrared rainbows may be more common, but an observer would need infrared night vision goggles to see them.[59]

Rainbows with different materials
A first order rainbow from water (left) and a sugar solution (right).

Droplets (or spheres) composed of materials with different refractive indices than plain water produce rainbows with different radius angles. Since salt water has a higher refractive index, a sea spray bow doesn't perfectly align with the ordinary rainbow, if seen at the same spot.[60] Tiny plastic or glass marbles may be used in road marking as a reflectors to enhance its visibility by drivers at night. Due to a much higher refractive index, rainbows observed on such marbles have a noticeably smaller radius.[61] One can easily reproduce such phenomena by sprinkling liquids of different refractive indices in the air, as illustrated in the photo.

The displacement of the rainbow due to different refractive indices can be pushed to a peculiar limit. For a material with a refractive index larger than 2, there is no angle fulfilling the requirements for the first order rainbow. For example, the index of refraction of diamond is about 2.4, so diamond spheres would produce rainbows starting from the second order, omitting the first order. In general, as the refractive index exceeds a number n+1, where n is a natural number, the critical incidence angle for n times internally reflected rays escapes the domain . This results in a rainbow of the n-th order shrinking to the antisolar point and vanishing.

Scientific history

The classical Greek scholar Aristotle (384–322 BC) was first to devote serious attention to the rainbow.[62] According to Raymond L. Lee and Alistair B. Fraser, "Despite its many flaws and its appeal to Pythagorean numerology, Aristotle's qualitative explanation showed an inventiveness and relative consistency that was unmatched for centuries. After Aristotle's death, much rainbow theory consisted of reaction to his work, although not all of this was uncritical."[63]

In Book I of Naturales Quaestiones (c. 65 AD), the Roman philosopher Seneca the Younger discusses various theories of the formation of rainbows extensively, including those of Aristotle. He notices that rainbows appear always opposite to the sun, that they appear in water sprayed by a rower, in the water spat by a fuller on clothes stretched on pegs or by water sprayed through a small hole in a burst pipe. He even speaks of rainbows produced by small rods (virgulae) of glass, anticipating Newton's experiences with prisms. He takes into account two theories: one, that the rainbow is produced by the sun reflecting in each water drop, the other, that it is produced by the sun reflected in a cloud shaped like a concave mirror; he favours the latter. He also discusses other phenomena related to rainbows: the mysterious "virgae" (rods), halos and parhelia.[64]

According to Hüseyin Gazi Topdemir, the Arab physicist and polymath Ibn al-Haytham (Alhazen; 965–1039), attempted to provide a scientific explanation for the rainbow phenomenon. In his Maqala fi al-Hala wa Qaws Quzah (On the Rainbow and Halo), al-Haytham "explained the formation of rainbow as an image, which forms at a concave mirror. If the rays of light coming from a farther light source reflect to any point on axis of the concave mirror, they form concentric circles in that point. When it is supposed that the sun as a farther light source, the eye of viewer as a point on the axis of mirror and a cloud as a reflecting surface, then it can be observed the concentric circles are forming on the axis." He was not able to verify this because his theory that "light from the sun is reflected by a cloud before reaching the eye" did not allow for a possible experimental verification.[65] This explanation was repeated by Averroes, and, though incorrect, provided the groundwork for the correct explanations later given by Kamāl al-Dīn al-Fārisī in 1309 and, independently, by Theodoric of Freiberg (c. 1250–c. 1311)—both having studied al-Haytham's Book of Optics.[66]

Ibn al-Haytham's contemporary, the Persian philosopher and polymath Ibn Sīnā (Avicenna; 980–1037), provided an alternative explanation, writing "that the bow is not formed in the dark cloud but rather in the very thin mist lying between the cloud and the sun or observer. The cloud, he thought, serves simply as the background of this thin substance, much as a quicksilver lining is placed upon the rear surface of the glass in a mirror. Ibn Sīnā would change the place not only of the bow, but also of the colour formation, holding the iridescence to be merely a subjective sensation in the eye."[67] This explanation, however, was also incorrect. Ibn Sīnā's account accepts many of Aristotle's arguments on the rainbow.[68]

In Song Dynasty China (960–1279), a polymath scholar-official named Shen Kuo (1031–1095) hypothesised—as a certain Sun Sikong (1015–1076) did before him—that rainbows were formed by a phenomenon of sunlight encountering droplets of rain in the air.[69] Paul Dong writes that Shen's explanation of the rainbow as a phenomenon of atmospheric refraction "is basically in accord with modern scientific principles."[70]

According to Nader El-Bizri, the Persian astronomer, Qutb al-Din al-Shirazi (1236–1311), gave a fairly accurate explanation for the rainbow phenomenon. This was elaborated on by his student, Kamāl al-Dīn al-Fārisī (1267–1319), who gave a more mathematically satisfactory explanation of the rainbow. He "proposed a model where the ray of light from the sun was refracted twice by a water droplet, one or more reflections occurring between the two refractions." An experiment with a water-filled glass sphere was conducted and al-Farisi showed the additional refractions due to the glass could be ignored in his model.[65][lower-alpha 3] As he noted in his Kitab Tanqih al-Manazir (The Revision of the Optics), al-Farisi used a large clear vessel of glass in the shape of a sphere, which was filled with water, in order to have an experimental large-scale model of a rain drop. He then placed this model within a camera obscura that has a controlled aperture for the introduction of light. He projected light unto the sphere and ultimately deduced through several trials and detailed observations of reflections and refractions of light that the colours of the rainbow are phenomena of the decomposition of light.

In Europe, Ibn al-Haytham's Book of Optics was translated into Latin and studied by Robert Grosseteste. His work on light was continued by Roger Bacon, who wrote in his Opus Majus of 1268 about experiments with light shining through crystals and water droplets showing the colours of the rainbow.[71] In addition, Bacon was the first to calculate the angular size of the rainbow. He stated that the rainbow summit can not appear higher than 42° above the horizon.[72] Theodoric of Freiberg is known to have given an accurate theoretical explanation of both the primary and secondary rainbows in 1307. He explained the primary rainbow, noting that "when sunlight falls on individual drops of moisture, the rays undergo two refractions (upon ingress and egress) and one reflection (at the back of the drop) before transmission into the eye of the observer."[73][74] He explained the secondary rainbow through a similar analysis involving two refractions and two reflections.

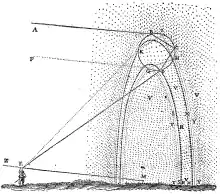
René Descartes' sketch of how primary and secondary rainbows are formed

Descartes' 1637 treatise, Discourse on Method, further advanced this explanation. Knowing that the size of raindrops did not appear to affect the observed rainbow, he experimented with passing rays of light through a large glass sphere filled with water. By measuring the angles that the rays emerged, he concluded that the primary bow was caused by a single internal reflection inside the raindrop and that a secondary bow could be caused by two internal reflections. He supported this conclusion with a derivation of the law of refraction (subsequently to, but independently of, Snell) and correctly calculated the angles for both bows. His explanation of the colours, however, was based on a mechanical version of the traditional theory that colours were produced by a modification of white light.[75][76]

Isaac Newton demonstrated that white light was composed of the light of all the colours of the rainbow, which a glass prism could separate into the full spectrum of colours, rejecting the theory that the colours were produced by a modification of white light. He also showed that red light is refracted less than blue light, which led to the first scientific explanation of the major features of the rainbow.[77] Newton's corpuscular theory of light was unable to explain supernumerary rainbows, and a satisfactory explanation was not found until Thomas Young realised that light behaves as a wave under certain conditions, and can interfere with itself.

Young's work was refined in the 1820s by George Biddell Airy, who explained the dependence of the strength of the colours of the rainbow on the size of the water droplets.[78] Modern physical descriptions of the rainbow are based on Mie scattering, work published by Gustav Mie in 1908.[79] Advances in computational methods and optical theory continue to lead to a fuller understanding of rainbows. For example, Nussenzveig provides a modern overview.[80]

Experiments
Round bottom flask rainbow demonstration experiment - Johnson 1882

Experiments on the rainbow phenomenon using artificial raindrops, i.e. water-filled spherical flasks, go back at least to Theodoric of Freiberg in the 14th century. Later, also Descartes studied the phenomenon using a Florence flask. A flask experiment known as Florence's rainbow is still often used today as an imposing and intuitively accessible demonstration experiment of the rainbow phenomenon.[81][82][83] It consists in illuminating (with parallel white light) a water-filled spherical flask through a hole in a screen. A rainbow will then appear thrown back / projected on the screen, provided the screen is large enough. Due to the finite wall thickness and the macroscopic character of the artificial raindrop, several subtle differences exist as compared to the natural phenomenon,[84][85] including slightly changed rainbow angles and a splitting of the rainbow orders.

A very similar experiment consists in using a cylindrical glass vessel filled with water or a solid transparent cylinder and illuminated either parallel to the circular base (i.e. light rays remaining at a fixed height while they transit the cylinder)[86][87] or under an angle to the base. Under these latter conditions the rainbow angles change relative to the natural phenomenon since the effective index of refraction of water changes (Bravais' index of refraction for inclined rays applies).[84][85]

Other experiments use small liquid drops,[51][52] see text above.

Culture
Main article: Rainbows in culture
Depiction of the rainbow in the Book of Genesis

Rainbows occur frequently in mythology, and have been used in the arts. One of the earliest literary occurrences of a rainbow is in the Book of Genesis chapter 9, as part of the flood story of Noah, where it is a sign of God's covenant to never destroy all life on earth with a global flood again. In Norse mythology, the rainbow bridge Bifröst connects the world of men (Midgard) and the realm of the gods (Asgard). Cuchavira was the god of the rainbow for the Muisca in present-day Colombia and when the regular rains on the Bogotá savanna were over, the people thanked him offering gold, snails and small emeralds. Some forms of Tibetan Buddhism or Dzogchen reference a rainbow body.[88] The Irish leprechaun's secret hiding place for his pot of gold is usually said to be at the end of the rainbow. This place is appropriately impossible to reach, because the rainbow is an optical effect which cannot be approached.

Rainbows appear in heraldry - in heraldry the rainbow proper consists of 4 bands of color (Or, Gules, Vert, Argent) with the ends resting on clouds.[89] Generalised examples in coat of arms include those of the towns of Regen and Pfreimd, both in Bavaria, Germany; and of Bouffémont, France; and of the 69th Infantry Regiment (New York) of the Army National Guard (USA).

Rainbow flags have been used for centuries. It was a symbol of the Cooperative movement in the German Peasants' War in the 16th century, of peace in Italy, and of gay pride and LGBT social movements since the 1970s. In 1994, Archbishop Desmond Tutu and President Nelson Mandela described newly democratic post-apartheid South Africa as the rainbow nation. The rainbow has also been used in technology product logos, including the Apple computer logo. Many political alliances spanning multiple political parties have called themselves a "Rainbow Coalition".

See also

Notes
  1. "A careful reading of Newton’s work indicates that the color he called indigo, we would normally call blue; his blue is then what we would name blue-green or cyan."[3]
  2. "Ex quo clarissime apparet, lumina variorum colorum varia esset refrangibilitate : idque eo ordine, ut color ruber omnium minime refrangibilis sit, reliqui autem colores, aureus, flavus, viridis, cæruleus, indicus, violaceus, gradatim & ex ordine magis magisque refrangibiles."[2]
  3. "approximation obtained by his model was good enough to allow him to ignore the effects of the glass container."[65]

References
  1. "Dr. Jeff Masters Rainbow Site". Archived from the original on 2015-01-29.
  2. Isaac Newton, Optice: Sive de Reflexionibus, Refractionibus, Inflexionibus & Coloribus Lucis Libri Tres, Propositio II, Experimentum VII, edition 1740
  3. Waldman, Gary (1983). Introduction to Light: The Physics of Light, Vision, and Color (2002 revised ed.). Mineola, New York: Dover Publications. p. 193. ISBN 978-0486421186.
  4. Walklet, Keith S. (2006). "Lunar Rainbows – When to View and How to Photograph a "Moonbow"". The Ansel Adams Gallery. Archived from the original on May 25, 2007. Retrieved 2007-06-07.
  5. "Why is the inside of a rainbow brighter than the outside sky?". WeatherQuesting. Archived from the original on May 28, 2013. Retrieved 2013-08-19.
  6. "Rainbow – A polarized arch?". Polarization.com. Archived from the original on 2013-09-09. Retrieved 2013-08-19.
  7. Burch, Paula E. "All About Hand Dyeing Q&A". Archived from the original on 24 April 2012. Retrieved 27 August 2012. (A number between 36 and 360 is in the order of 100)
  8. Gage, John (1994). Color and Meaning. University of California Press. p. 140. ISBN 978-0-520-22611-1.
  9. Allchin, Douglas. "Newton's Colors". SHiPS Resource Center. Archived from the original on 2014-09-29. Retrieved 2010-10-16.
  10. Hutchison, Niels (2004). "Music For Measure: On the 300th Anniversary of Newton's Opticks". Colour Music. Archived from the original on 2017-01-18. Retrieved 2017-04-07.
  11. Newton, Isaac (1704). Opticks.
  12. "Visible Spectrum Wikipedia Contributors, Wikipedia, The Free Encyclopedia accessed 11/17/2013 available at: Visible spectrum
  13. Cowley, Les. "Primary rainbow colours". Atmospheric Optics. Retrieved 27 August 2012.
  14. Rosch Heider, E. (1972). "Universals in color naming and memory". Journal of Experimental Psychology. 93 (1): 10–20. doi:10.1037/h0032606. PMID 5013326.
  15. Dawkins, Richard (2005). The ancestor's tale: a pilgrimage to the dawn of evolution.
  16. Roberson, Debi; Davies, Ian; Davidoff, Jules (September 2000). "Color categories are not universal: Replications and new evidence from a stone-age culture" (PDF). Journal of Experimental Psychology: General. 129 (3): 369–398. doi:10.1037/0096-3445.129.3.369. PMID 11006906.
  17. "About Rainbows". Eo.ucar.edu. Archived from the original on 2013-08-18. Retrieved 2013-08-19.
  18. Cowley, Les. "Sea Water Rainbow". Atmospheric Optics. Retrieved 2007-06-07.
  19. Cowley, Les. "Zero order glow". Atmospheric Optics. Archived from the original on 2013-01-13. Retrieved 2011-08-08.
  20. Anon (7 November 2014). "Why are rainbows curved as semicircles?". Ask the van. The Board of Trustees at the University of Illinois. Archived from the original on 2 October 2015. Retrieved 13 April 2015.
  21. "How to see a whole circle rainbow – EarthSky.org". earthsky.org. Archived from the original on 2013-10-04.
  22. "USATODAY.com – Look down on the rainbow". usatoday30.usatoday.com.
  23. Anon (29 March 2004). "Solution, Week 81, Rainbows" (PDF). Harvard University Department of Physics. Archived (PDF) from the original on 8 October 2016. Retrieved 13 June 2016.
  24. http://hyperphysics.phy-astr.gsu.edu/hbase/atmos/imgatm/lpath2.gif
  25. "Secondary rainbow". www.atoptics.co.uk.
  26. See:
    • Alexander of Aphrodisias, Commentary on Book IV of Aristotle's Meteorology (also known as: Commentary on Book IV of Aristotle's De Meteorologica or On Aristotle's Meteorology 4), commentary 41.
    • Raymond L. Lee and Alistair B. Fraser, The Rainbow Bridge: Rainbows in Art, Myth, and Science (University Park, Pennsylvania: Pennsylvania State University Press, 2001), pp. 110–111.
  27. "Atmospheric Optics: Twinned rainbows". Atoptics.co.uk. 2002-06-03. Retrieved 2013-08-19.
  28. See:
  29. Sadeghi, Iman; Munoz, Adolfo; Laven, Philip; Jarosz, Wojciech; Seron, Francisco; Gutierrez, Diego; Jensen, Henrik Wann (2012). "Physically-based simulation of rainbows" (PDF). ACM Transactions on Graphics. 31: 1–12. CiteSeerX 10.1.1.296.3051. doi:10.1145/2077341.2077344.
  30. "Triple-split rainbow observed and photographed in Japan, August 2012". blog.meteoros.de. 2015-03-12. Archived from the original on 2015-04-02. Retrieved 2015-03-12.
  31. "Can you ever see the whole circle of a rainbow? | Earth". EarthSky. 2012-12-15. Archived from the original on 2013-10-04. Retrieved 2013-10-04.
  32. Philip Laven (2012-08-04). "Circular rainbows". Philiplaven.com. Archived from the original on 2013-10-05. Retrieved 2013-10-04.
  33. "APOD: 2014 September 30 – A Full Circle Rainbow over Australia". apod.nasa.gov. Archived from the original on 2015-01-25.
  34. "OPOD – 360° Rainbow". www.atoptics.co.uk.
  35. "Supernumerary Rainbows". www.atoptics.co.uk.
  36. "Supernumerary Rainbows and drop size". www.atoptics.co.uk.
  37. "Fogbow droplet size effect". www.atoptics.co.uk.
  38. See:
  39. Les Cowley (Atmospheric Optics). "Bows everywhere!". Retrieved 13 April 2015.
  40. Nemiroff, R.; Bonnell, J., eds. (12 September 2007). "Six Rainbows Across Norway". Astronomy Picture of the Day. NASA. Retrieved 2007-06-07.
  41. "Atmospheric Optics: Reflection rainbows formation". Atoptics.co.uk. Retrieved 2013-08-19.
  42. "Dawn Red Rainbows Arizona – OPOD". atoptics.co.uk.
  43. "Untitled Document". www.atoptics.co.uk.
  44. "3rd & 4th order rainbows". www.atoptics.co.uk.
  45. Großmann, Michael; Schmidt, Elmar; Haußmann, Alexander (1 Oct 2011). "Photographic evidence for the third-order rainbow". Applied Optics. 50 (28): F134–F141. Bibcode:2011ApOpt..50F.134G. doi:10.1364/AO.50.00F134. ISSN 1559-128X. PMID 22016237.
  46. "Triple Rainbows Exist, Photo Evidence Shows, ScienceDaily.com, Oct. 5, 2011". Sciencedaily.com. 2011-10-06. Archived from the original on 2013-10-04. Retrieved 2013-08-19.
  47. Theusner, Michael (1 Oct 2011). "Photographic observation of a natural fourth-order rainbow". Applied Optics. 50 (28): F129–F133. Bibcode:2011ApOpt..50F.129T. doi:10.1364/AO.50.00F129. ISSN 1559-128X. PMID 22016236.
  48. "Short Sharp Science: First ever image of fourth-order rainbow". www.newscientist.com. Archived from the original on 2017-07-11.
  49. {{cite web|url=http://www.weatherscapes.com/quinary/%7Ctitle=Observations of the quinary rainbow|website=www.weatherscapes.com|url-status=live|archive-url=https://web.archive.org/web/20150103142928/http://www.weatherscapes.com/quinary/%7Carchive-date=2015-01-03}
  50. Billet, Felix (1868). "Mémoire sur les Dix-neuf premiers arcs-en-ciel de l'eau" [Memoir on the first nineteen rainbows]. Annales Scientifiques de l'École Normale Supérieure. 1 (5): 67–109. doi:10.24033/asens.43.
  51. Walker, Jearl (1977). "How to create and observe a dozen rainbows in a single drop of water". Scientific American. 237 (July): 138–144 + 154. Bibcode:1977SciAm.237a.138W. doi:10.1038/scientificamerican0777-138. Archived from the original on 2011-08-14. Retrieved 2011-08-08.
  52. J.D. Walker, “Mysteries of rainbows, notably their rare supernumerary arcs,” Sci. Am. 242(6), 174–184 (1980).
  53. Ng, P. H.; Tse, M. Y.; Lee, W. K. (1998). "Observation of high-order rainbows formed by a pendant drop". Journal of the Optical Society of America B. 15 (11): 2782. Bibcode:1998JOSAB..15.2782N. doi:10.1364/JOSAB.15.002782.
  54. "Moonbow – Lunar Rainbow". www.atoptics.co.uk. Archived from the original on 2008-04-21. Retrieved 2015-06-28.
  55. See:
  56. Les Cowley. Observing Halos – Getting Started Atmospheric Optics, accessed 3 December 2013.
  57. "Circumzenithal Arc". www.atoptics.co.uk.
  58. Cowley, Les. "Circumhorizontal arc". Atmospheric Optics. Retrieved 2007-04-22.
  59. Science@NASA. "Rainbows on Titan". Archived from the original on 2008-09-21. Retrieved 2008-11-25.
  60. Cowley, Les. "Sea Water Rainbow". Atmospheric Optics. Retrieved 2016-11-10.
  61. Cowley, Les. "Glass Bead Bows". Atmospheric Optics. Retrieved 2016-11-10.
  62. "The Internet Classics Archive – Meteorology by Aristotle". classics.mit.edu. Archived from the original on 2014-02-18.
  63. Raymond L. Lee; Alistair B. Fraser (2001). The rainbow bridge: rainbows in art, myth, and science. Penn State Press. p. 109. ISBN 978-0-271-01977-2.
  64. Seneca, Lucius Anneus (1 April 2014). Delphi Complete Works of Seneca the Younger (Illustrated). Book I (Delphi Ancient Classics Book 27 ed.). Delphi Classics.
  65. O'Connor, J.J.; Robertson, E.F. (November 1999). "Kamal al-Din Abu'l Hasan Muhammad Al-Farisi". MacTutor History of Mathematics archive, University of St Andrews. Archived from the original on 2007-03-25. Retrieved 2007-06-07.
  66. Nader El-Bizri 'Ibn al-Haytham et le problème de la couleur', Oriens-Occidens: Cahiers du centre d'histoire des sciences et des philosophies arabes et médiévales, C.N.R.S. 7 (2009), pp. 201–226.
  67. Carl Benjamin Boyer (1954). "Robert Grosseteste on the Rainbow". Osiris. 11: 247–258. doi:10.1086/368581.
  68. Raymond L. Lee; Alistair B. Fraser (2001). The rainbow bridge: rainbows in art, myth, and science. Penn State Press. pp. 141–144. ISBN 978-0-271-01977-2.
  69. Sivin, Nathan (1995). Science in Ancient China: Researches and Reflections Brookfield, Vermont: VARIORUM. III: Ashgate Publishing. p. 24.
  70. Dong, Paul (2000). China's Major Mysteries: Paranormal Phenomena and the Unexplained in the People's Republic. San Francisco: China Books and Periodicals, Inc. p. 72. ISBN 978-0-8351-2676-2.
  71. Davidson, Michael W. (August 1, 2003). "Roger Bacon (1214–1294)". Florida State University. Archived from the original on August 30, 2006. Retrieved 2006-08-10.
  72. Raymond L. Lee; Alistair B. Fraser (2001). The rainbow bridge: rainbows in art, myth, and science. p. 156. ISBN 978-0-271-01977-2.
  73. Lindberg, David C (Summer 1966). "Roger Bacon's Theory of the Rainbow: Progress or Regress?". Isis. 57 (2): 235. doi:10.1086/350116.
  74. Theodoric of Freiberg (c. 1304–1310) De iride et radialibus impressionibus (On the rainbow and the impressions of radiance).
  75. Boyer, Carl B. (1952). "Descartes and the Radius of the Rainbow". Isis. 43 (2): 95–98. doi:10.1086/349399.
  76. Gedzelman, Stanley David (1989). "Did Kepler's Supplement to Witelo Inspire Descartes' Theory of the Rainbow?". Bulletin of the American Meteorological Society. 70 (7): 750–751. Bibcode:1989BAMS...70..750G. doi:10.1175/1520-0477(1989)070<0750:DKSTWI>2.0.CO;2. ISSN 1520-0477.
  77. O'Connor, J.J.; Robertson, E.F. (January 2000). "Sir Isaac Newton". University of St. Andrews. Archived from the original on 2007-06-10. Retrieved 2007-06-19.
  78. See:
  79. G. Mie (1908) "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen" Archived 2012-03-02 at the Wayback Machine (Contributions to the optics of turbid media, especially of colloidal metal solutions), Annalen der Physik, 4th series, 25 (3): 377–445.
  80. Nussenzveig, H. Moyses (1977). "The Theory of the Rainbow". Scientific American. 236 (4): 116. Bibcode:1977SciAm.236d.116N. doi:10.1038/scientificamerican0477-116.
  81. “Florence's Rainbow”, Harvard Natural Sciences Lecture Demonstrations, link Archived 2017-01-08 at the Wayback Machine
  82. “Rainbow: Refraction of white light by a liquid sphere.”, U.C. Berkeley Physics Lecture Demonstrations, link Archived 2017-01-08 at the Wayback Machine
  83. “The Rainbow,”J.B. Calvert, link Archived 2016-05-24 at the Wayback Machine, retrieved: 10/01/2016
  84. “Revisiting the round bottom flask rainbow experiment.”, M. Selmke and S. Selmke, arXiv, link Archived 2017-01-08 at the Wayback Machine
  85. Pictures and Raytracings under "Alexander's dark band (or bright band?)", M. Selmke, link Archived 2017-01-08 at the Wayback Machine
  86. G. Casini and A. Covello, “The ”rainbow” in the drop,” Am. J. Phys. 80(11), 1027–1034 (2012).
  87. “Primary and Secondary Bow of a Rainbow”, U.C. Berkeley Physics Lecture Demonstrations, link Archived 2017-01-08 at the Wayback Machine
  88. Ray, Reginald (2001). Secret of the Vajra World: The Tantric Buddhism of Tibet. Shambhala Publications. p. 323. ISBN 9781570627729.
  89. "Rainbow", mistholme.com

Further reading
  • Greenler, Robert (1980). Rainbows, Halos, and Glories. Cambridge University Press. ISBN 978-0-19-521833-6.
  • Lee, Raymond L. & Alastair B. Fraser (2001). The Rainbow Bridge: Rainbows in Art, Myth and Science. New York: Pennsylvania State University Press and SPIE Press. ISBN 978-0-271-01977-2.
  • Lynch, David K.; Livingston, William (2001). Color and Light in Nature (2nd ed.). Cambridge University Press. ISBN 978-0-521-77504-5.
  • Minnaert, Marcel G.J.; Lynch, David K.; Livingston, William (1993). Light and Color in the Outdoors. Springer-Verlag. ISBN 978-0-387-97935-9.
  • Minnaert, Marcel G.J.; Lynch, David K.; Livingston, William (1973). The Nature of Light and Color in the Open Air. Dover Publications. ISBN 978-0-486-20196-2.
  • Naylor, John; Lynch, David K.; Livingston, William (2002). Out of the Blue: A 24-Hour Skywatcher's Guide. Cambridge University Press. ISBN 978-0-521-80925-2.
  • Boyer, Carl B. (1987). The Rainbow, From Myth to Mathematics. Princeton University Press. ISBN 978-0-691-08457-2.
  • Graham, Lanier F., ed. (1976). The Rainbow Book. Berkeley, California: Shambhala Publications and The Fine Arts Museums of San Francisco. (Large format handbook for the Summer 1976 exhibition The Rainbow Art Show which took place primarily at the De Young Museum but also at other museums. The book is divided into seven sections, each coloured a different colour of the rainbow.)
  • De Rico, Ul (1978). The Rainbow Goblins. Thames & Hudson. ISBN 978-0-500-27759-1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.