Rectified truncated tetrahedron
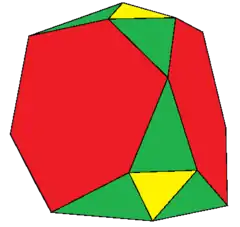
The rectified truncated tetrahedron is a polyhedron, constructed as a rectified truncated tetrahedron. It has 20 faces: 4 equilateral triangles, 12 isosceles triangles, and 4 regular hexagons.
| Rectified truncated tetrahedron | |
|---|---|
 | |
| Schläfli symbol | rt{3,3} |
| Conway notation | atT |
| Faces | 20: 4 {3} 12 { }∨( ) 4 {6} |
| Edges | 48 |
| Vertices | 12+18 |
| Symmetry group | Td, [3,3], (*332) order 24 |
| Rotation group | T, [3,3]+, (332), order 12 |
| Dual polyhedron | Joined truncated tetrahedron |
| Properties | convex |
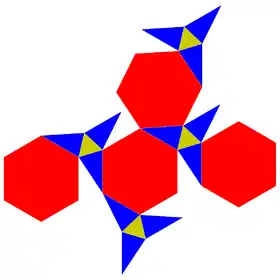 Net | |
Topologically, the triangles corresponding to the tetrahedron's vertices are always equilateral, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the equilateral triangles, having different but alternating angles, causing the other triangles to be isosceles instead.
Related polyhedra
The rectified truncated tetrahedron can be seen in sequence of rectification and truncation operations from the tetrahedron. Further truncation, and alternation operations creates two more polyhedra:
| Name | Truncated tetrahedron |
Rectified truncated tetrahedron |
Truncated rectified truncated tetrahedron |
Snub rectified truncated tetrahedron |
|---|---|---|---|---|
| Coxeter | tT | rtT | trtT | srtT |
| Conway | atT | btT | stT | |
| Image |  |
 |
 |
 |
| Conway | dtT = kT | jtT | mtT | gtT |
| Dual |  |
 |
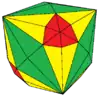 |
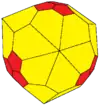 |
See also
References
- Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.