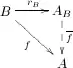Reflective subcategory

In mathematics, a full subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint.[1]^:91 This adjoint is sometimes called a reflector, or localization.[2] Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.

Informally, a reflector acts as a kind of completion operation. It adds in any "missing" pieces of the structure in such a way that reflecting it again has no further effect.

Definition

A full subcategory A of a category B is said to be reflective in B if for each B-object B there exists an A-object ${\displaystyle A_{B}}$ and a B-morphism ${\displaystyle r_{B}\colon B\to A_{B}}$ such that for each B-morphism ${\displaystyle f\colon B\to A}$ to an A-object ${\displaystyle A}$ there exists a unique A-morphism ${\displaystyle {\overline {f}}\colon A_{B}\to A}$ with ${\displaystyle {\overline {f}}\circ r_{B}=f}$.

The pair ${\displaystyle (A_{B},r_{B})}$ is called the A-reflection of B. The morphism ${\displaystyle r_{B}}$ is called the A-reflection arrow. (Although often, for the sake of brevity, we speak about ${\displaystyle A_{B}}$ only as being the A-reflection of B).

This is equivalent to saying that the embedding functor ${\displaystyle E\colon \mathbf {A} \hookrightarrow \mathbf {B} }$ is a right adjoint. The left adjoint functor ${\displaystyle R\colon \mathbf {B} \to \mathbf {A} }$ is called the reflector. The map ${\displaystyle r_{B}}$ is the unit of this adjunction.

The reflector assigns to ${\displaystyle B}$ the A-object ${\displaystyle A_{B}}$ and ${\displaystyle Rf}$ for a B-morphism ${\displaystyle f}$ is determined by the commuting diagram

If all A-reflection arrows are (extremal) epimorphisms, then the subcategory A is said to be (extremal) epireflective. Similarly, it is bireflective if all reflection arrows are bimorphisms.

All these notions are special case of the common generalization—${\displaystyle E}$-reflective subcategory, where ${\displaystyle E}$ is a class of morphisms.

The ${\displaystyle E}$-reflective hull of a class A of objects is defined as the smallest ${\displaystyle E}$-reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.

An anti-reflective subcategory is a full subcategory A such that the only objects of B that have an A-reflection arrow are those that are already in A.

Dual notions to the above-mentioned notions are coreflection, coreflection arrow, (mono)coreflective subcategory, coreflective hull, anti-coreflective subcategory.

Examples

Algebra

• The category of abelian groups Ab is a reflective subcategory of the category of groups, Grp. The reflector is the functor that sends each group to its abelianization. In its turn, the category of groups is a reflective subcategory of the category of inverse semigroups.[3]
• Similarly, the category of commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the commutator ideal. This is used in the construction of the symmetric algebra from the tensor algebra.
• Dually, the category of anti-commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the anti-commutator ideal. This is used in the construction of the exterior algebra from the tensor algebra.
• The category of fields is a reflective subcategory of the category of integral domains (with injective ring homomorphisms as morphisms). The reflector is the functor that sends each integral domain to its field of fractions.
• The category of abelian torsion groups is a coreflective subcategory of the category of abelian groups. The coreflector is the functor sending each group to its torsion subgroup.
• The categories of elementary abelian groups, abelian p-groups, and p-groups are all reflective subcategories of the category of groups, and the kernels of the reflection maps are important objects of study; see focal subgroup theorem.
• The category of groups is a coreflective subcategory of the category of monoids: the right adjoint maps a monoid to its group of units.[4]

Topology

• The category of Kolmogorov spaces (T₀ spaces) is a reflective subcategory of Top, the category of topological spaces, and the Kolmogorov quotient is the reflector.
• The category of completely regular spaces CReg is a reflective subcategory of Top. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
• The category of all compact Hausdorff spaces is a reflective subcategory of the category of all Tychonoff spaces (and of the category of all topological spaces[2]^:140). The reflector is given by the Stone–Čech compactification.
• The category of all complete metric spaces with uniformly continuous mappings is a reflective subcategory of the category of metric spaces. The reflector is the completion of a metric space on objects, and the extension by density on arrows.[1]^:90

Functional analysis

• The category of Banach spaces is a reflective subcategory of the category of normed spaces and bounded linear operators. The reflector is the norm completion functor.

Category theory

• For any Grothendieck site (C, J), the topos of sheaves on (C, J) is a reflective subcategory of the topos of presheaves on C, with the special further property that the reflector functor is left exact. The reflector is the sheafification functor a : Presh(C) → Sh(C, J), and the adjoint pair (a, i) is an important example of a geometric morphism in topos theory.

Properties

• The components of the counit are isomorphisms.[2]^:140[1]
• If D is a reflective subcategory of C, then the inclusion functor D → C creates all limits that are present in C.[2]^:141
• A reflective subcategory has all colimits that are present in the ambient category.[2]^:141
• The monad induced by the reflector/localization adjunction is idempotent.[2]^:158

Notes

1. Mac Lane, Saunders, 1909-2005. (1998). Categories for the working mathematician (2nd ed.). New York: Springer. p. 89. ISBN 0387984038. OCLC 37928530.CS1 maint: multiple names: authors list (link)
2. Riehl, Emily (2017-03-09). Category theory in context. Mineola, New York. p. 140. ISBN 9780486820804. OCLC 976394474.
3. Lawson (1998), p. 63, Theorem 2.
4. "coreflective subcategory in nLab". ncatlab.org. Retrieved 2019-04-02.

References

• Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstract and Concrete Categories (PDF). New York: John Wiley & Sons.
• Peter Freyd, Andre Scedrov (1990). Categories, Allegories. Mathematical Library Vol 39. North-Holland. ISBN 978-0-444-70368-2.
• Herrlich, Horst (1968). Topologische Reflexionen und Coreflexionen. Lecture Notes in Math. 78. Berlin: Springer.
• Mark V. Lawson (1998). Inverse semigroups: the theory of partial symmetries. World Scientific. ISBN 978-981-02-3316-7.