Relief (feature selection)
Relief is an algorithm developed by Kira and Rendell in 1992 that takes a filter-method approach to feature selection that is notably sensitive to feature interactions.[1][2] It was originally designed for application to binary classification problems with discrete or numerical features. Relief calculates a feature score for each feature which can then be applied to rank and select top scoring features for feature selection. Alternatively, these scores may be applied as feature weights to guide downstream modeling. Relief feature scoring is based on the identification of feature value differences between nearest neighbor instance pairs. If a feature value difference is observed in a neighboring instance pair with the same class (a 'hit'), the feature score decreases. Alternatively, if a feature value difference is observed in a neighboring instance pair with different class values (a 'miss'), the feature score increases. The original Relief algorithm has since inspired a family of Relief-based feature selection algorithms (RBAs), including the ReliefF[3] algorithm. Beyond the original Relief algorithm, RBAs have been adapted to (1) perform more reliably in noisy problems,[4] (2) generalize to multi-class problems[4] (3) generalize to numerical outcome (i.e. regression) problems,[5] and (4) to make them robust to incomplete (i.e. missing) data.[4]
To date, the development of RBA variants and extensions has focused on four areas; (1) improving performance of the 'core' Relief algorithm, i.e. examining strategies for neighbor selection and instance weighting, (2) improving scalability of the 'core' Relief algorithm to larger feature spaces through iterative approaches, (3) methods for flexibly adapting Relief to different data types, and (4) improving Relief run efficiency.[6]
Their strengths are that they are not dependent on heuristics, they run in low-order polynomial time, and they are noise-tolerant and robust to feature interactions, as well as being applicable for binary or continuous data; however, it does not discriminate between redundant features, and low numbers of training instances fool the algorithm.
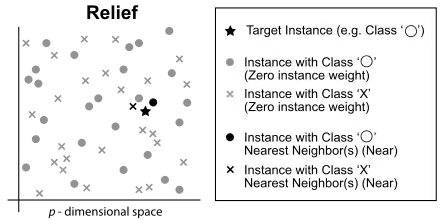
Relief Algorithm
Take a data set with n instances of p features, belonging to two known classes. Within the data set, each feature should be scaled to the interval [0 1] (binary data should remain as 0 and 1). The algorithm will be repeated m times. Start with a p-long weight vector (W) of zeros.
At each iteration, take the feature vector (X) belonging to one random instance, and the feature vectors of the instance closest to X (by Euclidean distance) from each class. The closest same-class instance is called 'near-hit', and the closest different-class instance is called 'near-miss'. Update the weight vector such that
Thus the weight of any given feature decreases if it differs from that feature in nearby instances of the same class more than nearby instances of the other class, and increases in the reverse case.
After m iterations, divide each element of the weight vector by m. This becomes the relevance vector. Features are selected if their relevance is greater than a threshold τ.
Kira and Rendell's experiments[2] showed a clear contrast between relevant and irrelevant features, allowing τ to be determined by inspection. However, it can also be determined by Chebyshev's inequality for a given confidence level (α) that a τ of 1/sqrt(α*m) is good enough to make the probability of a Type I error less than α, although it is stated that τ can be much smaller than that.
Relief was also described as generalizable to multinomial classification by decomposition into a number of binary problems.
ReliefF Algorithm
Kononenko et al. propose a number of updates to Relief.[3] Firstly, they find the near-hit and near-miss instances using the Manhattan (L1) norm rather than the Euclidean (L2) norm, although the rationale is not specified. Furthermore, they found taking the absolute differences between xi and near-hiti, and xi and near-missi to be sufficient when updating the weight vector (rather than the square of those differences).
Reliable probability estimation
Rather than repeating the algorithm m times, implement it exhaustively (i.e. n times, once for each instance) for relatively small n (up to one thousand). Furthermore, rather than finding the single nearest hit and single nearest miss, which may cause redundant and noisy attributes to affect the selection of the nearest neighbors, ReliefF searches for k nearest hits and misses and averages their contribution to the weights of each feature. k can be tuned for any individual problem.
Incomplete data
In ReliefF, the contribution of missing values to the feature weight is determined using the conditional probability that two values should be the same or different, approximated with relative frequencies from the data set. This can be calculated if one or both features are missing.
Multi-class problems
Rather than use Kira and Rendell's proposed decomposition of a multinomial classification into a number of binomial problems, ReliefF searches for k near misses from each different class and averages their contributions for updating W, weighted with the prior probability of each class.
Other Relief-based Algorithm Extensions/Derivatives
The following RBAs are arranged chronologically from oldest to most recent.[6] They include methods for improving (1) the core Relief algorithm concept, (2) iterative approaches for scalability, (3) adaptations to different data types, (4) strategies for computational efficiency, or (5) some combination of these goals. For more on RBAs see these book chapters [7][8][9] or this most recent review paper.[6]
RRELIEFF
Robnik-Šikonja and Kononenko propose further updates to ReliefF, making it appropriate for regression.[5]
Relieved-F
Introduced deterministic neighbor selection approach and a new approach for incomplete data handling.[10]
Iterative Relief
Implemented method to address bias against non-monotonic features. Introduced the first iterative Relief approach. For the first time, neighbors were uniquely determined by a radius threshold and instances were weighted by their distance from the target instance.[11]
I-RELIEF
Introduced sigmoidal weighting based on distance from target instance.[12][13] All instance pairs (not just a defined subset of neighbors) contributed to score updates. Proposed an on-line learning variant of Relief. Extended the iterative Relief concept. Introduced local-learning updates between iterations for improved convergence.[14]
TuRF (a.k.a. Tuned ReliefF)
Specifically sought to address noise in large feature spaces through the recursive elimination of features and the iterative application of ReliefF.[15]
Evaporative Cooling ReliefF
Similarly seeking to address noise in large feature spaces. Utilized an iterative `evaporative' removal of lowest quality features using ReliefF scores in association with mutual information.[16]
EReliefF (a.k.a. Extended ReliefF)
Addressing issues related to incomplete and multi-class data.[17]
VLSReliefF (a.k.a. Very Large Scale ReliefF)
Dramatically improves the efficiency of detecting 2-way feature interactions in very large feature spaces by scoring random feature subsets rather than the entire feature space.[18]
ReliefMSS
Introduced calculation of feature weights relative to average feature 'diff' between instance pairs.[19]
SURF
SURF identifies nearest neighbors (both hits and misses) based on a distance threshold from the target instance defined by the average distance between all pairs of instances in the training data.[20] Results suggest improved power to detect 2-way epistatic interactions over ReliefF.
SURF* (a.k.a. SURFStar)
SURF*[21] extends the SURF[20] algorithm to not only utilized 'near' neighbors in scoring updates, but 'far' instances as well, but employing inverted scoring updates for 'far instance pairs. Results suggest improved power to detect 2-way epistatic interactions over SURF, but an inability to detect simple main effects (i.e. univariate associations).[22]
SWRF*
SWRF* extends the SURF* algorithm adopting sigmoid weighting to take distance from the threshold into account. Also introduced a modular framework for further developing RBAs called MoRF.[23]
MultiSURF* (a.k.a. MultiSURFStar)
MultiSURF*[24] extends the SURF*[21] algorithm adapting the near/far neighborhood boundaries based on the average and standard deviation of distances from the target instance to all others. MultiSURF* uses the standard deviation to define a dead-band zone where 'middle-distance' instances do not contribute to scoring. Evidence suggests MultiSURF* performs best in detecting pure 2-way feature interactions.[22]
ReliefSeq
Introduces a feature-wise adaptive k parameter for more flexibly detecting univariate effects and interaction effects.[25]
MultiSURF
MultiSURF[22] simplifies the MultiSURF*[24] algorithm by preserving the dead-band zone, and target-instance-centric neighborhood determination, but eliminating the 'far' scoring. Evidence suggests MultiSURF to be a well rounded option, able to detect 2-way and 3-way interactions, as well as simple univariate associations.[22] Also introduced the RBA software package called ReBATE that includes implementations of (Relief, ReliefF, SURF, SURF*, MultiSURF*, MultiSURF, and TuRF).
STIR
STIR [26][27] reformulates and slightly adjusts the original Relief formula by incorporating sample variance of the nearest neighbor distances into the attribute importance estimation. This variance permits the calculation of statistical significance of features and adjustment for multiple testing of Relief-based scores. Currently, STIR supports binary outcome variable but will soon be extended to multi-state and continuous outcome.
RBA Applications
Different RBAs have been applied to feature selection in a variety of problem domains.
See also
References
- Kira, Kenji and Rendell, Larry (1992). The Feature Selection Problem: Traditional Methods and a New Algorithm. AAAI-92 Proceedings.
- Kira, Kenji and Rendell, Larry (1992) A Practical Approach to Feature Selection, Proceedings of the Ninth International Workshop on Machine Learning, p249-256
- Kononenko, Igor et al. Overcoming the myopia of inductive learning algorithms with RELIEFF (1997), Applied Intelligence, 7(1), p39-55
- Kononenko, Igor (1994-04-06). "Estimating attributes: Analysis and extensions of RELIEF". Machine Learning: ECML-94. Lecture Notes in Computer Science. 784. Springer, Berlin, Heidelberg. pp. 171–182. doi:10.1007/3-540-57868-4_57. ISBN 978-3540578680. Missing or empty
|title=(help) - Robnik-Šikonja, Marko, and Kononenko, Igor (1997). An adaptation of Relief for attribute estimation in regression. Machine Learning: Proceedings of the Fourteenth International Conference (ICML’97) (p296-304)
- Urbanowicz, Ryan J.; Meeker, Melissa; LaCava, William; Olson, Randal S.; Moore, Jason H. (2018). "Relief-Based Feature Selection: Introduction and Review". Journal of Biomedical Informatics. 85: 189–203. arXiv:1711.08421. Bibcode:2017arXiv171108421U. doi:10.1016/j.jbi.2018.07.014. PMC 6299836. PMID 30031057.
- Kononenko, Igor, Robnik-Sikonja, Marko (2007-10-29). Non-Myopic Feature Quality Evaluation with (R)ReliefF. pp. 169–192. doi:10.1201/9781584888796-9.
- Moore, Jason H. (2015). "Epistasis Analysis Using ReliefF". Epistasis. Methods in Molecular Biology. 1253. Humana Press, New York, NY. pp. 315–325. doi:10.1007/978-1-4939-2155-3_17. ISBN 9781493921546. PMID 25403540.
- Todorov, Alexandre (2016-07-08). An Overview of the RELIEF Algorithm and Advancements. MIT Press. ISBN 9780262034685.
- Kohavi, Ron; John, George H (1997-12-01). "Wrappers for feature subset selection". Artificial Intelligence. 97 (1–2): 273–324. doi:10.1016/S0004-3702(97)00043-X. ISSN 0004-3702.
- Draper, B.; Kaito, C.; Bins, J. (June 2003). "Iterative Relief". 2003 Conference on Computer Vision and Pattern Recognition Workshop. 6: 62. doi:10.1109/CVPRW.2003.10065. S2CID 17599624.
- Sun, Yijun; Li, Jian (2006-06-25). "Iterative RELIEF for feature weighting". Proceedings of the 23rd international conference on Machine learning - ICML '06. ACM. pp. 913–920. CiteSeerX 10.1.1.387.7424. doi:10.1145/1143844.1143959. ISBN 978-1595933836. S2CID 1102692.
- Sun, Y. (June 2007). "Iterative RELIEF for Feature Weighting: Algorithms, Theories, and Applications". IEEE Transactions on Pattern Analysis and Machine Intelligence. 29 (6): 1035–1051. doi:10.1109/TPAMI.2007.1093. ISSN 0162-8828. PMID 17431301. S2CID 14087053.
- Sun, Y.; Todorovic, S.; Goodison, S. (September 2010). "Local-Learning-Based Feature Selection for High-Dimensional Data Analysis". IEEE Transactions on Pattern Analysis and Machine Intelligence. 32 (9): 1610–1626. doi:10.1109/TPAMI.2009.190. ISSN 0162-8828. PMC 3445441. PMID 20634556.
- Moore, Jason H.; White, Bill C. (2007-04-11). Tuning ReliefF for Genome-Wide Genetic Analysis. Evolutionary Computation,Machine Learning and Data Mining in Bioinformatics. Lecture Notes in Computer Science. 4447. Springer, Berlin, Heidelberg. pp. 166–175. doi:10.1007/978-3-540-71783-6_16. ISBN 9783540717829.
- McKinney, B.A.; Reif, D.M.; White, B.C.; Crowe, J.E.; Moore, J.H. (2007-08-15). "Evaporative cooling feature selection for genotypic data involving interactions". Bioinformatics. 23 (16): 2113–2120. doi:10.1093/bioinformatics/btm317. ISSN 1367-4803. PMC 3988427. PMID 17586549.
- Park, H.; Kwon, H. C. (August 2007). Extended Relief Algorithms in Instance-Based Feature Filtering. Sixth International Conference on Advanced Language Processing and Web Information Technology (ALPIT 2007). pp. 123–128. doi:10.1109/ALPIT.2007.16. ISBN 978-0-7695-2930-1. S2CID 15296546.
- Eppstein, M. J.; Haake, P. (September 2008). Very large scale ReliefF for genome-wide association analysis. 2008 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology. pp. 112–119. doi:10.1109/CIBCB.2008.4675767. ISBN 978-1-4244-1778-0. S2CID 9296768.
- Chikhi, Salim; Benhammada, Sadek (2009-11-04). "ReliefMSS: a variation on a feature ranking ReliefF algorithm". International Journal of Business Intelligence and Data Mining. 4 (3/4): 375. doi:10.1504/ijbidm.2009.029085. S2CID 15242788.
- Greene, Casey S.; Penrod, Nadia M.; Kiralis, Jeff; Moore, Jason H. (2009-09-22). "Spatially Uniform ReliefF (SURF) for computationally-efficient filtering of gene-gene interactions". BioData Mining. 2 (1): 5. doi:10.1186/1756-0381-2-5. ISSN 1756-0381. PMC 2761303. PMID 19772641.
- Greene, Casey S.; Himmelstein, Daniel S.; Kiralis, Jeff; Moore, Jason H. (2010-04-07). The Informative Extremes: Using Both Nearest and Farthest Individuals Can Improve Relief Algorithms in the Domain of Human Genetics. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Lecture Notes in Computer Science. 6023. Springer, Berlin, Heidelberg. pp. 182–193. doi:10.1007/978-3-642-12211-8_16. ISBN 9783642122101.
- Urbanowicz, Ryan J.; Olson, Randal S.; Schmitt, Peter; Meeker, Melissa; Moore, Jason H. (2017-11-22). "Benchmarking Relief-Based Feature Selection Methods for Bioinformatics Data Mining". arXiv:1711.08477. Bibcode:2017arXiv171108477U. PMID 30030120.
- Stokes, Matthew E.; Visweswaran, Shyam (2012-12-03). "Application of a spatially-weighted Relief algorithm for ranking genetic predictors of disease". BioData Mining. 5 (1): 20. doi:10.1186/1756-0381-5-20. ISSN 1756-0381. PMC 3554553. PMID 23198930.
- Granizo-Mackenzie, Delaney; Moore, Jason H. (2013-04-03). Multiple Threshold Spatially Uniform ReliefF for the Genetic Analysis of Complex Human Diseases. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Lecture Notes in Computer Science. 7833. Springer, Berlin, Heidelberg. pp. 1–10. doi:10.1007/978-3-642-37189-9_1. ISBN 9783642371882.
- McKinney, Brett A.; White, Bill C.; Grill, Diane E.; Li, Peter W.; Kennedy, Richard B.; Poland, Gregory A.; Oberg, Ann L. (2013-12-10). "ReliefSeq: A Gene-Wise Adaptive-K Nearest-Neighbor Feature Selection Tool for Finding Gene-Gene Interactions and Main Effects in mRNA-Seq Gene Expression Data". PLOS ONE. 8 (12): e81527. Bibcode:2013PLoSO...881527M. doi:10.1371/journal.pone.0081527. ISSN 1932-6203. PMC 3858248. PMID 24339943.
- Le, Trang; Urbanowicz, Ryan; Moore, Jason; McKinney, Brett (18 September 2018). "STatistical Inference Relief (STIR) feature selection". Bioinformatics. 35 (8): 1358–1365. doi:10.1093/bioinformatics/bty788. PMC 6477983. PMID 30239600.
- Le, Trang (1 November 2018). "STIR Poster". Figshare. doi:10.6084/m9.figshare.7241417. Retrieved 24 January 2019.