Rippling

Rippling[1] refers to a group of meta-level heuristics, developed primarily in the Mathematical Reasoning Group in the School of Informatics at the University of Edinburgh, and most commonly used to guide inductive proofs in automated theorem proving systems. Rippling may be viewed as a restricted form of rewrite system, where special object level annotations are used to ensure fertilization upon the completion of rewriting, with a measure decreasing requirement ensuring termination for any set of rewrite rules and expression.

History

Raymond Aubin was the first person to use the term "rippling out" whilst working on his 1976 PhD thesis[2] at the University of Edinburgh. He recognised a common pattern of movement during the rewriting stage of inductive proofs. Alan Bundy later turned this concept on its head by defining rippling to be this pattern of movement, rather than a side effect.

Since then, "rippling sideways", "rippling in" and "rippling past" were coined, so the term was generalised to rippling. Rippling continues to be developed at Edinburgh, and elsewhere, as of 2007.

Rippling has been applied to many problems traditionally viewed as being hard in the inductive theorem proving community, including Bledsoe's limit theorems and a proof of the Gordon microprocessor, a miniature computer developed by Michael J. C. Gordon and his team at Cambridge.

Overview

Very often, when attempting to prove a proposition, we are given a source expression and a target expression, which differ only by the inclusion of a few extra syntactic elements.

This is especially true in inductive proofs, where the given expression is taken to be the inductive hypothesis, and the target expression the inductive conclusion. Usually, the differences between the hypothesis and conclusion are only minor, perhaps the inclusion of a successor function (e.g., +1) around the induction variable.

At the start of rippling the differences between the two expressions, known as wave-fronts in rippling parlance, are identified. Typically these differences prevent the completion of the proof and need to be "moved away". The target expression is annotated to distinguish the wavefronts (differences) and skeleton (common structure) between the two expressions. Special rules, called wave rules, can then be used in a terminating fashion to manipulate the target expression until the source expression can be used to complete the proof.

Example

We aim to show that the addition of natural numbers is commutative. This is an elementary property, and the proof is by routine induction. Nevertheless, the search space for finding such a proof may become quite large.

Typically, the base case of any inductive proof is solved by methods other than rippling. For this reason, we will concentrate on the step case. Our step case takes the following form, where we have chosen to use x as the induction variable:

We may also possess several rewrite rules, drawn from lemmas, inductive definitions or elsewhere, that can be used to form wave-rules. Suppose we have the following three rewrite rules:

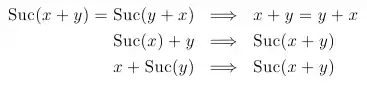
then these can be annotated, to form:

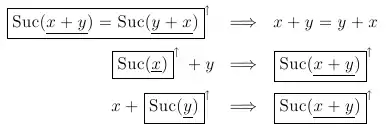
Note that all these annotated rules preserve the skeleton (x + y = y + x, in the first case and x + y in the second/third). Now, annotating the inductive step case, gives us:

And we are all set to perform rippling:

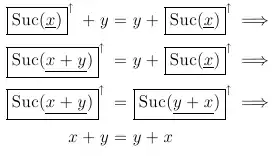
Note that the final rewrite causes all wave-fronts to disappear, and we may now apply fertilization, the application of the inductive hypotheses, to complete the proof.

References
  1. Alan Bundy; David Basin; Dieter Hutter; Andrew Ireland (2005). Rippling: Meta-Level Guidance for Mathematical Reasoning. Cambridge Tracts in Theoretical Computer Science. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511543326. ISBN 0-521-83449-X.
  2. Aubin, Raymond (1976), Mechanizing Structural Induction, EDI-INF-PHD, 76–002, University of Edinburgh, hdl:1842/6649

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.