Structural reliability

Structural reliability is about applying reliability engineering theories to buildings and, more generally, structural analysis.[1][2] Reliability is also used as a probabilistic measure of structural safety. The reliability of a structure is defined as the probability of complement of failure ${\displaystyle ({\text{Reliability}}=1-{\text{Probability of Failure}})}$. The failure occurs when the total applied load is larger than the total resistance of the structure. Structural reliability has become known as a design philosophy in the twenty-first century, and it might replace traditional deterministic ways of design[3] and maintenance.[2]

Failure occurs when loads (s) are larger than resistance (R)

Theory

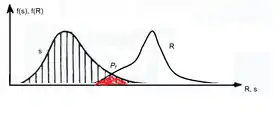
In structural reliability studies, both loads and resistances are modeled as probabilistic variables. Using this approach the probability of failure of a structure is calculated. When loads and resistances are explicit and have their own independent function, the probability of failure could be formulated as follows.[1][2]

${\displaystyle P_{f}=\int _{0}^{\infty }F_{R}(s)f_{s}(s)\,ds\qquad \mathrm {(1)} }$

where ${\displaystyle P_{f}}$is the probability of failure, ${\displaystyle F_{R}(s)}$is the cumulative distribution function of resistance (R), and ${\displaystyle f_{s}(s)}$is the probability density of load (S).

However, in most cases, the distribution of loads and resistances are not independent and the probability of failure is defined via the following more general formula.

${\displaystyle P_{f}=\int \int \int _{G(X)}f_{X}(X)\,dX\qquad \mathrm {(2)} }$

where 𝑋 is the vector of the basic variables, and G(X) that is called is the limit state function could be a line, surface or volume that the integral is taken on its surface.

Solution approaches

Analytical solutions

In some cases when load and resistance are explicitly expressed (such as equation (1) above), and their distributions are normal , the integral of equation (1) has a closed-form solution as follows.

${\displaystyle p_{f}=1-\Phi (\beta ),}$${\displaystyle \beta ={\frac {\mu _{R}-\mu _{S}}{\sqrt {\sigma _{R}^{2}+\sigma _{S}^{2}}}}\qquad \mathrm {(3)} }$

Simulation

In most cases load and resistance are not normally distributed. Therefore, solving the integrals of equations (1) and (2) analytically is impossible. Using Monte Carlo simulation is an approach that could be used in such cases.[1][4]

References

1. Melchers, R. E. (2002), “Structural Reliability Analysis and Prediction,” 2nd Ed., John Wiley, Chichester, UK.
2. Piryonesi, Sayed Madeh; Tavakolan, Mehdi (9 January 2017). "A mathematical programming model for solving cost-safety optimization (CSO) problems in the maintenance of structures". KSCE Journal of Civil Engineering. 21 (6): 2226–2234. doi:10.1007/s12205-017-0531-z.
3. Choi, S. K., Grandhi, R., & Canfield, R. A. (2006). Reliability-based structural design. Springer Science & Business Media.
4. Okasha, N. M., & Frangopol, D. M. (2009). Lifetime-oriented multi-objective optimization of structural maintenance considering system reliability, redundancy and life-cycle cost using GA. Structural Safety, 31(6), 460-474.