Top-nodes algorithm

The top-nodes algorithm is an algorithm for managing a resource reservation calendar. The algorithm has been first published in 2003,[1] and has been improved in 2009.[2] It is used when a resource is shared among many users (for example bandwidth in a telecommunication link, or disk capacity in a large data center).

The algorithm allows users to:

  • check if an amount of resource is available during a specific period of time,
  • reserve an amount of resource for a specific period of time,
  • delete a previous reservation,
  • move the calendar forward (the calendar covers a defined duration, and it must be moved forward as time goes by).

Principle

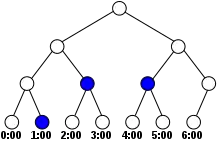
The calendar is stored as a binary tree where leaves represent elementary time periods. Other nodes represent the period of time covered by all their descendants.

Example of a seven-hour calendar (with elementary periods of one hour)

The period of time covered by a reservation is represented by a set of "top-nodes". This set is the minimal set of nodes that exactly cover the reservation period of time.

A node of the binary tree is a "top-node" for a given reservation if

  • all its descendants are inside the reservation period of time, and
  • it is the root node, or at least one descendant of the parent node is outside of the reservation period of time.
Top-nodes for a reservation from 1:00 to 5:59

The following value is stored in each node:

q(node) = max(q(left child), q(right child))
          + total amount of reserved resource for all reservations having this node as a "top-node"

(for code optimization, the two parts of this sum are usually stored separately.)

Performance

The advantage of this algorithm is that the time to register a new resource reservation depends only on the calendar size (it does not depend on the total number of reservations).

Let n be the number of elementary periods in the calendar.

The maximal number of "top-nodes" for a given reservation is 2.log n.

  • to check if an amount of resource is available during a specific period of time : O(log n)
  • to reserve an amount of resource for a specific period of time : O(log n)
  • to delete a previous reservation : O(log n)
  • to move the calendar forward : O(log n + M.log n)

where M is the number of reservations that are active during the added calendar periods.

(M = 0 if reservations are not allowed after the end of the calendar.)

References
  1. Related US patent (the algorithm is in the public domain since 2008)
  2. Improved top-nodes algorithm
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.