Visvalingam–Whyatt algorithm

The Visvalingam–Whyatt algorithm, also known as the Visvalingam's algorithm, is an algorithm that decimates a curve composed of line segments to a similar curve with fewer points.

Idea

Given a polygonal chain (often called a Polyline), the algorithm attempts to find a similar chain composed of fewer points.

Points are assigned an importance based on local conditions, and points are removed from the least important to most important.

In Visvalingam's algorithm, the importance is related to the triangular area added by each point.

Algorithm

Given a chain of 2d points ${\displaystyle \left\{p_{i}\right\}=\left\{{\begin{bmatrix}x_{i}\\y_{i}\end{bmatrix}}\right\}}$, the importance of each interior point is computed by finding the area of the triangle formed by it and its immediate neighbors. This can be done quickly using a matrix determinant.[1] Alternatively, the equivalent formula below can be used[2]

${\displaystyle A_{i}={\frac {1}{2}}\left|x_{i-1}y_{i}+x_{i}y_{i+1}+x_{i+1}y_{i-1}-x_{i-1}y_{i+1}-x_{i}y_{i-1}-x_{i+1}y_{i}\right|}$

The minimum importance point ${\displaystyle p_{i}}$ is located and marked for removal (note that ${\displaystyle A_{i-1}}$ and ${\displaystyle A_{i+1}}$ will need to be recomputed). This process is repeated until either the desired number of points is reached, or the contribution of the least important point is too large to neglect.

Pseudocode

TODO(Phoritual)

function TriangularArea(Point p1, Point p2, Point p3)
    // Return the area enclosed by the triangle p1-p2-p3
    return abs(
        p1.x * p2.y + p2.x * p3.y + p3.x * p1.y
        - p1.x * p3.y - p2.x * p1.y - p3.x * p2.y
    ) / 2
end
    
function VisvalingamWhyatt(List[Point] ps)
    // TODO(woursler): Write pseudocode
    // Return the result
    return ResultList[]
end

Advantages

• The algorithm is easy to understand and explain, but is often competitive with much more complex approaches.
• With the use of a priority queue, the algorithm is performant on large inputs, since the importance of each point can be computed using only its neighbors, and removing a point only requires recomputing the importance of two other points.
• It is simple to generalize to higher dimensions, since the area of the triangle between points has a consistent meaning.

Disadvantages

Points with equivalent "importance" may be of different topological importance.

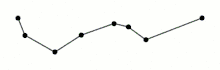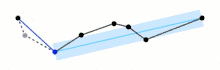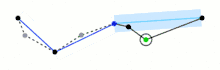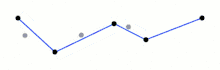
• The algorithm does not differentiate between sharp spikes and shallow features, meaning that it will clean up sharp spikes that may be important.
• The algorithm simplifies the entire length of the curve evenly, meaning that curves with high and low detail areas will likely have their fine details eroded.

See also

• Curve fitting

Alternative algorithms for line simplification include:

• Ramer–Douglas–Peucker
• Reumann–Witkam
• Opheim simplification
• Lang simplification
• Zhao–Saalfeld algorithm

References

1. "6.5 – Applications of Matrices and Determinants". people.richland.edu. Retrieved 2020-07-07.
2. "Untitled Document". people.richland.edu. Retrieved 2020-07-07.

External links

• 1995 Paper proposing the method.