Wallis's conical edge

Wallis's conical edge is a ruled surface given by the parametric equations:

${\displaystyle x=v\cos u,\quad y=v\sin u,\quad z=c{\sqrt {a^{2}-b^{2}\cos ^{2}u}}.}$

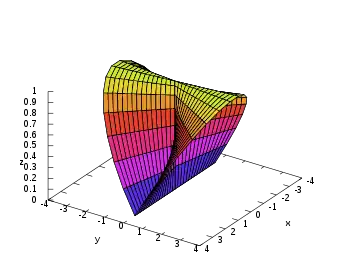
Figure 1. Wallis's Conical Edge with a=b=c=1

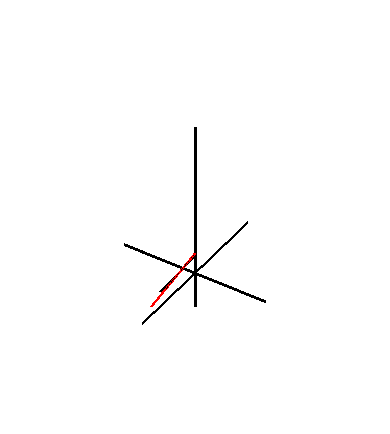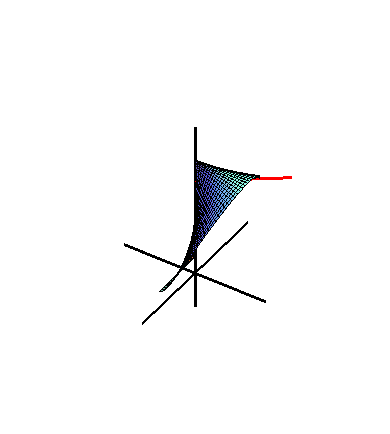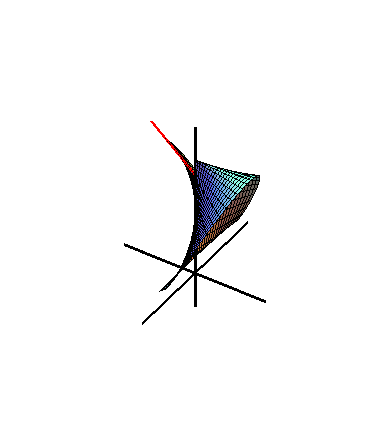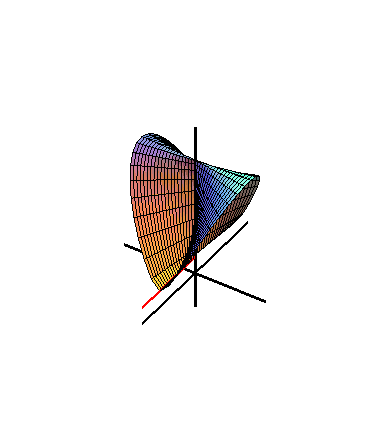
Figure 2. Wallis's Conical Edge with a=1.01,b=c=1

where a, b and c are constants.

Wallis's conical edge is also a kind of right conoid.

Figure 2 shows that the Wallis's conical edge is generated by a moving line.

Wallis's conical edge is named after the English mathematician John Wallis, who was one of the first to use Cartesian methods to study conic sections.[1]

See also

• Ruled surface
• Right conoid

References

• A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, Florida:CRC Press, 2006. (ISBN 978-1-58488-448-4)

External links

• Wallis's Conical Edge from MathWorld.