Zolotarev polynomials
In mathematics, Zolotarev polynomials are polynomials used in approximation theory. They are sometimes used as an alternative to the Chebyshev polynomials where accuracy of approximation near the origin is of less importance. Zolotarev polynomials differ from the Chebyshev polynomials in that two of the coefficients are fixed in advance rather than allowed to take on any value. The Chebyshev polynomials of the first kind are a special case of Zolotarev polynomials. These polynomials were introduced by Russian mathematician Yegor Ivanovich Zolotarev in 1868.
Definition and properties
Zolotarev polynomials of degree in are of the form
where is a prescribed value for and the are otherwise chosen such that the deviation of from zero is minimum in the interval .[1]
A subset of Zolotarev polynomials can be expressed in terms of Chebyshev polynomials of the first kind, . For
then
For values of greater than the maximum of this range, Zolotarev polynomials can be expressed in terms of elliptic functions. For , the Zolotarev polynomial is identical to the equivalent Chebyshev polynomial. For negative values of , the polynomial can be found from the polynomial of the positive value,[2]
The Zolotarev polynomial can be expanded into a sum of Chebyshev polynomials using the relationship[3]
In terms of Jacobi elliptic functions
The original solution to the approximation problem given by Zolotarev was in terms of Jacobi elliptic functions. Zolotarev gave the general solution where the number of zeroes to the left of the peak value () in the interval is not equal to the number of zeroes to the right of this peak (). The degree of the polynomial is . For many applications, is used and then only need be considered. The general Zolotarev polynomials are defined as[5]
- where
- is the Jacobi eta function
- is the incomplete elliptic integral of the first kind
- is the quater-wave complete elliptic integral of the first kind. That is, [6]
- is the Jacobi elliptic modulus
- is the Jacobi elliptic sine.
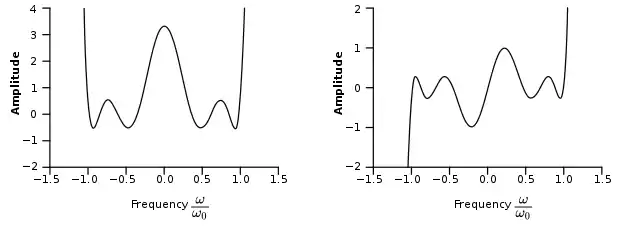
The variation of the function within the interval [−1,1] is equiripple except for one peak which is larger than the rest. The position and width of this peak can be set independently. The position of the peak is given by[7]
-
- where
- is the Jacobi elliptic cosine
- is the Jacobi delta amplitude
- is the Jacobi zeta function
- is as defined above.
The height of the peak is given by[8]
-
- where
- is the incomplete elliptic integral of the third kind
- is the position on the left limb of the peak which is the same height as the equiripple peaks.
Applications
The polynomials were introduced by Yegor Ivanovich Zolotarev in 1868 as a means of uniformly approximating polynomials of degree on the interval [−1,1]. Pafnuty Chebyshev had shown in 1858 that could be approximated in this interval with a polynomial of degree at most with an error of . In 1868, Zolotarev showed that could be approximated with a polynomial of degree at most , two degrees lower. The error in Zolotarev's method is given by,[11]
The procedure was further developed by Naum Achieser in 1956.[12]
Zolotarev polynomials are used in the design of Achieser-Zolotarev filters. They were first used in this role in 1970 by Ralph Levy in the design of microwave waveguide filters.[13] Achieser-Zolotarev filters are similar to Chebyshev filters in that they have an equal ripple attenuation through the passband, except that the attenuation exceeds the preset ripple for the peak closest to the origin.[14]
Zolotarev polynomials can be used to synthesise the radiation patterns of linear antenna arrays, first suggested by D.A. McNamara in 1985. The work was based on the filter application with beam angle used as the variable instead of frequency. The Zolotarev beam pattern has equal-level sidelobes.[15]
References
- Pinkus, pp. 463–464
- Pinkus, p. 464
- Zahradnik & Vlček, p. 58
- Cameron et al., p. 400
- Zahradnik & Miroslav, pp. 57–58
- Beebe, p. 624
- Zahradnik & Miroslav, p. 58
- Zahradnik & Miroslav, p. 58
- Beebe, p. 679
- Beebe, p. 625
- Newman & Reddy, p. 310
- Newman & Reddy, pp. 310, 316
- Hansen, p.87
- Cameron et al., p. 399
- Hansen, p.87
Bibliography
- Achieser, Naum, Hymnan, C.J. (trans), Theory of Approximation, New York: Frederick Ungar Publishing, 1956. Dover reprint 2013 ISBN 0486495434.
- Beebe, Nelson H.F., he Mathematical-Function Computation Handbook, Springer, 2017 ISBN 3319641107.
- Cameron, Richard J.; Kudsia, Chandra M.; Mansour, Raafat R., Microwave Filters for Communication Systems, John Wiley & Sons, 2018 ISBN 1118274342.
- Hansen, Robert C., Phased Array Antennas, Wiley, 2009 ISBN 0470529172.
- McNamara, D.A., "Optimum monopulse linear array excitations using Zolotarev Polynomials", Electron, vol. 21, iss. 16, pp. 681–682, August 1985.
- Newman, D.J., Reddy, A.R., "Rational approximations to II", Canadian Journal of Mathematics, vol. 32, no. 2, pp. 310–316, April 1980.
- Pinkus, Allan, "Zolotarev polynomials", in, Hazewinkel, Michiel (ed), Encyclopaedia of Mathematics, Supplement III, Springer Science & Business Media, 2001 ISBN 1402001983.
- Vlček, Miroslav, Unbehauen, Rolf, "Zolotarev polynomials and optimal FIR filters", IEEE Transactions on Signal Processing, vol. 47 , iss. 3, pp. 717–730, March 1999 (corrections July 2000).
- Zahradnik, Pavel; Vlček, Miroslav, "Analytical design of 2-D narrow bandstop FIR filters", pp. 56–63 in, Computational Science — ICCS 2004: Proceedings of the 4th International Conference, Bubak, Marian; van Albada, Geert D.; Sloot, Peter M.A.; Dongarra, Jack (eds), Springer Science & Business Media, 2004 ISBN 3540221298.