Alexandroff plank

Alexandroff plank in topology, an area of mathematics, is a topological space that serves as an instructive example.

Definition

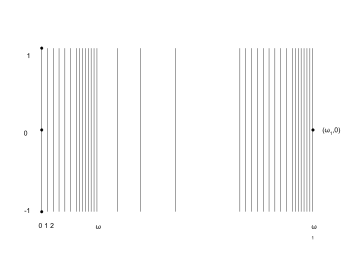
Diagram of Alexandroff plank

The construction of the Alexandroff plank starts by defining the topological space ${\displaystyle (X,\tau )}$ to be the Cartesian product of ${\displaystyle [0,\omega _{1}]}$ and ${\displaystyle [-1,1]}$, where ${\displaystyle \omega _{1}}$ is the first uncountable ordinal, and both carry the interval topology. The topology ${\displaystyle \tau }$ is extended to a topology ${\displaystyle \sigma }$ by adding the sets of the form

${\displaystyle U(\alpha ,n)=\{p\}\cup (\alpha ,\omega _{1}]\times (0,1/n)}$

where ${\displaystyle p=(\omega _{1},0)\in X}$.

The Alexandroff plank is the topological space ${\displaystyle (X,\sigma )}$.

It is called plank for being constructed from a subspace of the product of two spaces.

Properties

The space ${\displaystyle (X,\sigma )}$ satisfies that:

1. is Urysohn, since ${\displaystyle (X,\tau )}$ is regular. The space ${\displaystyle (X,\sigma )}$ is not regular, since ${\displaystyle C=\{(\alpha ,0)\mid \alpha <\omega _{1}\}}$ is a closed set not containing ${\displaystyle (\omega _{1},0)}$, while every neighbourhood of ${\displaystyle C}$ intersects every neighbourhood of ${\displaystyle (\omega _{1},0)}$.
2. is semiregular, since each basis rectangle in the topology ${\displaystyle \tau }$ is a regular open set and so are the sets ${\displaystyle U(\alpha ,n)}$ defined above with which the topology was expanded.
3. is not countably compact, since the set ${\displaystyle \{(\omega _{1},-1/n)\mid n=2,3,\ldots \}}$ has no upper limit point.
4. is not metacompact, since if ${\displaystyle \{V_{\alpha }\}}$ is a covering of the ordinal space ${\displaystyle [0,\omega _{1})}$ with not point-finite refinement, then the covering ${\displaystyle \{U_{\alpha }\}}$ of ${\displaystyle X}$ defined by ${\displaystyle U_{1}=\{(0,\omega _{1})\}\cup ([0,\omega _{1}]\times (0,1])}$, ${\displaystyle U_{2}=[0,\omega _{1}]\times [-1,0)}$, and ${\displaystyle U_{\alpha }=V_{\alpha }\times [-1,1]}$ has not point-finite refinement.

References

• Lynn Arthur Steen and J. Arthur Seebach, Jr., Counterexamples in Topology. Springer-Verlag, New York, 1978. Reprinted by Dover Publications, New York, 1995. ISBN 0-486-68735-X (Dover edition).
• S. Watson, The Construction of Topological Spaces. Recent Progress in General Topology, Elsevier, 1992.