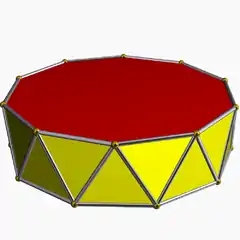
Decagonal antiprism

In geometry, the decagonal antiprism is the eighth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.

Uniform decagonal antiprism
Type	Prismatic uniform polyhedron
Elements	F = 22, E = 40 V = 20 (χ = 2)
Faces by sides	20{3}+2{10}
Schläfli symbol	s{2,20} sr{2,10}
Wythoff symbol	| 2 2 10
Coxeter diagram
Symmetry group	D10d, [2^+,20], (2*10), order 40
Rotation group	D10, [10,2]^+, (10.2.2), order 20
References	U77(h)
Dual	Decagonal trapezohedron
Properties	convex
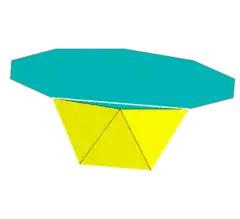Vertex figure 3.3.3.10

Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.

In the case of a regular 10-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.

If faces are all regular, it is a semiregular polyhedron.

See also

Family of uniform n-gonal antiprisms
Polyhedron image												...	Apeirogonal antiprism
Spherical tiling image												Plane tiling image
Vertex configuration n.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

External links

• Weisstein, Eric W. "Antiprism". MathWorld.
• Decagonal Antiprism: 3-d polyhedron model
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model
  • Conway Notation for Polyhedra Try: "A10"