Ferrimagnetism
A Ferrimagnetic material is material that has populations of atoms with opposing magnetic moments, as in antiferromagnetism. For ferrimagnetic materials these moments are unequal in magnitude so a Spontaneous magnetization remains.[1] This can for example happen when the populations consist out of different atoms or ions (such as Fe2+ and Fe3+).
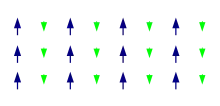
Ferrimagnetism has often been confused with ferromagnetism. The oldest known magnetic substance magnetite (Fe3O4) was classified as a ferromagnet before Louis Néel discovered ferrimagnetism in 1948.[2] Since the discovery numerous uses have been found for ferrimagnetic materials, such as for hard drives and in Biomedicine.
History
Until the twentieth century, all naturally magnetic substances were called ferromagnets. In 1936 Louis Néel published a paper proposing the existence of a new form of cooperative magnetism he called antiferromagnetism.[3] While working with Mn2Sb, French physicist Charles Guillaud discoverd that the current theories on magnetism were not adequate to explain the behaviour of the material, and made a model to explain the behaviour.[4] In 1948, Néel published a paper about a third type of cooperative magnetism, based on the assumptions in Guillaud's model. He called it ferrimagnetism. In 1970, Néels was awarded for his work in magnetism with the Nobel Prize in Physics.[5]
Physical origin
Ferrimagnetism has the same physical origins as Ferromagnetism and Antiferromagnetism. In ferrimagnetic materials the magnetisation is also caused by a combination of dipole-dipole interactions and the exchange interaction caused by the Pauli exclusion principle. The main difference with ferromagnetism and antiferromagnetism is that there are different types of atoms in the unit cell. An example of this can be seen The figure on the right. Here the atoms with a smaller magnetic moment point in the opposite direction of the larger moments. So here there is an anti-ferromagnetic ordering but there is still a non-zero magnetic moment. Ferrimagnets have a critical temperature above which they become paramagnetic just as ferromagnets do.[6] At this temperature (called the Curie temperature) there is a second order phase transition[7] and the system can no longer maintain a spontaneous magnetisation. This is because at higher temperatures the thermal motion is big enough so that it outcompetes the tendency of the dipoles to align.
Derivation
There are various ways to describe ferrimagnets, the simplest of which is with Mean-field theory. In mean field theory the field acting on the atoms can be written as:
Where is the Applied magnetic field field and is field caused by the interactions between the atoms. The following assumption then is: Here is the average magnetization of the lattice and is the molecular field coefficient. When we allow and to be position and orientation dependent we can then write it in the form:
Here is the field acting on the ith substructure and is the molecular field coefficient between the ith and the kth substructure. For a diatomic lattice we can designate two types of sites, A and B. the number of magnetic ions per unit volume, the fraction of the magnetic ions on the A sites and on the B sites. This then gives:
It can be shown that and that unless the structures are identical. favours a parallel alignment of and , while favours an anti-parallel alignment. For ferrimagnets so it will be convenient to take as a positive quantity and write the minus sing explicitly in front of it. For the total fields on A and B this then gives:
Furthermore we will introduce the parameters and which give the ratio between the strenghts of the interactions. At last we will introduce the reduced magnetization's:
With the spin of the ith element. This then gives for the fields:
The solutions to these equations (omitted here) are then given by
Where is the Brillouin function. The simplest case to solve now is . Since . This then gives the following pair of equations:
With and . These equations do not have a known analytical solution so these must be solved numerically to find the temperature dependence of .
Effects of temperature
Unlike ferromagnetism, the shapes of the magnetization curves of ferrimagnetism can take many different shapes depending on the strength of the interactions and the relative abundance of atoms. The most notable of which is that the direction of the magnetization can change sign while heating op from Absolute zero to the critical temperature, and that the magnetization increases while increasing the temperature to the critical temperature, which both cannot occur for ferromagnetic materials. These temperature dependencies have also been experimentally observed in NiFe2/5Cr8/5O4[8] and Li1/2Fe5/4Ce5/4O4.[9]
The point where the net magnetisation is 0 for temperatures below the Curie temperature at which the opposing magnetic moments are equal, resulting in a net magnetic moment of zero is called the magnetization compensation point. This compensation point is observed easily in garnets and rare-earth–transition-metal alloys (RE-TM). Furthermore, ferrimagnets may also have an Angular momentum compensation point, at which the net angular momentum vanishes. This compensation point is a crucial point for achieving high speed magnetization reversal in magnetic memory devices.
Effect of external fields
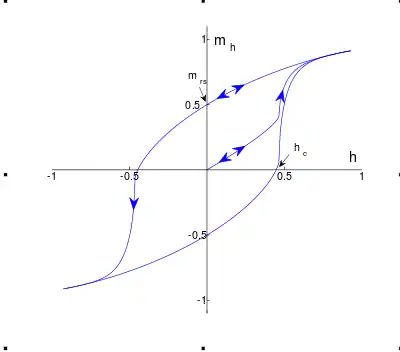
When ferrimagnets are exposed to an external magnetic field, they display what is called Magnetic hysteresis , the magnetic behaviour depends on the history of the magnet. They also know a saturation magnetisation , this magnetisation is reached when the external field is strong enough to make all the moments align in the same direction. When this point is reached, the magnetisation cannot increase as there are no more moments to align. Once you decrease the external field back to , the magnetisation of the ferrimagnet will not go back to but will rather stay magnetised. This is effect is often used in applications of magnets. When the external field is then put in the opposite direction the magnet will demagnetise further until it will eventually reach a magnetisation of . This behaviour results in what is called a hysteresis loop.[10]
Properties and Uses
Ferrimagnetic materials have high resistivity and have anisotropic properties. The anisotropy is actually induced by an external applied field. When this applied field aligns with the magnetic dipoles, it causes a net magnetic dipole moment and causes the magnetic dipoles to precess at a frequency controlled by the applied field, called Larmor or precession frequency. As a particular example, a microwave signal circularly polarized in the same direction as this precession strongly interacts with the magnetic dipole moments; when it is polarized in the opposite direction, the interaction is very low. When the interaction is strong, the microwave signal can pass through the material. This directional property is used in the construction of microwave devices like isolators, circulators, and gyrators. Ferrimagnetic materials are also used to produce optical isolators and circulators. Ferrimagnetic minerals in various rock types are used to study ancient geomagnetic properties of Earth and other planets. That field of study is known as paleomagnetism. Furthermore it has been shown that ferrimagnets such as Magnetite can be used for Thermal energy storage.[11]
Examples
The oldest known magnetic material, Magnetite, is a ferrimagnetic substance. The Tetrahedral and Octahedral sites exhibit opposite spin. Other known ferrimagnetic materials include yttrium iron garnet (YIG); cubic ferrites composed of iron oxides with other elements such as aluminum, cobalt, nickel, manganese, and zinc; and hexagonal ferrites such as PbFe12O19 and BaFe12O19 and pyrrhotite, Fe1−xS.[12]
Ferrimagnetism can also occur in single-molecule magnets. A classic example is a dodecanuclear manganese molecule with an effective spin S = 10 derived from antiferromagnetic interaction on Mn(IV) metal centres with Mn(III) and Mn(II) metal centres.[13]
See also
References
- Spaldin, Nicola A. (2011). Magnetic materials : fundamentals and applications (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-88669-7. OCLC 607986416.
- Néel, M. Louis (1948). "Propriétés magnétiques des ferrites ; ferrimagnétisme et antiferromagnétisme" (PDF). Annales de Physique. 12 (3): 137–198. doi:10.1051/anphys/194812030137. ISSN 0003-4169.
- Néel, Louis (1936). "Propriétés magnétiques de l'état métallique et énergie d'interaction entre atomes magnétiques". Annales de physique. 11 (5): 232–279. doi:10.1051/anphys/193611050232. ISSN 0003-4169.
- Smart, J. Samuel (September 1955). "The Néel Theory of Ferrimagnetism". American Journal of Physics. 23 (6): 356–370. doi:10.1119/1.1934006. ISSN 0002-9505.
- "The Nobel Prize in Physics 1970". NobelPrize.org. Retrieved 2021-01-26.
- Simon, Steven H. (21 June 2013). The Oxford Solid State Basics (First ed.). Oxford. ISBN 978-0-19-150210-1. OCLC 851099021.
- Blundell, Stephen; Blundell, Katherine M. (2010). Concepts in thermal physics (2nd ed.). Oxford: Oxford University Press. ISBN 978-0-19-956209-1. OCLC 607907330.
- Tsushima, Tachiro (August 1963). "Magnetic Properties of Ferrite-Chromite Series of Nickel and Cobalt". Journal of the Physical Society of Japan. 18 (8): 1162–1166. doi:10.1143/jpsj.18.1162. ISSN 0031-9015.
- Gorter, E. W.; Schulkes, J. A. (1953-05-01). "Reversal of Spontaneous Magnetization as a Function of Temperature in LiFeCr Spinels". Physical Review. 90 (3): 487–488. doi:10.1103/physrev.90.487.2. ISSN 0031-899X.
- Soler, M. A. G.; Paterno, L. G. (2017-01-01), Da Róz, Alessandra L.; Ferreira, Marystela; de Lima Leite, Fábio; Oliveira, Osvaldo N. (eds.), "6 - Magnetic Nanomaterials", Nanostructures, William Andrew Publishing, pp. 147–186, doi:10.1016/b978-0-323-49782-4.00006-1, ISBN 978-0-323-49782-4, retrieved 2021-01-25
- Grosu, Yaroslav; Faik, Abdessamad; Ortega-Fernández, Iñigo; D'Aguanno, Bruno (March 2017). "Natural Magnetite for thermal energy storage: Excellent thermophysical properties, reversible latent heat transition and controlled thermal conductivity". Solar Energy Materials and Solar Cells. 161: 170–176. doi:10.1016/j.solmat.2016.12.006.
- Klein, C. and Dutrow, B., Mineral Science, 23rd ed., Wiley, p. 243.
- Sessoli, Roberta; Tsai, Hui Lien; Schake, Ann R.; Wang, Sheyi; Vincent, John B.; Folting, Kirsten; Gatteschi, Dante; Christou, George; Hendrickson, David N. (1993). "High-spin molecules: [Mn12O12(O2CR)16(H2O)4]". J. Am. Chem. Soc. 115 (5): 1804–1816. doi:10.1021/ja00058a027.
External links
 Media related to Ferrimagnetism at Wikimedia Commons
Media related to Ferrimagnetism at Wikimedia Commons