Heptagonal bipyramid
The heptagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an heptagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. The resulting solid has 14 triangular faces, 9 vertices and 21 edges.[1][2]
| Heptagonal bipyramid | |
|---|---|
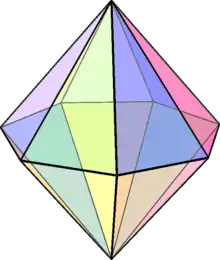 | |
| Type | bipyramid |
| Faces | 14 triangles |
| Edges | 21 |
| Vertices | 9 |
| Schläfli symbol | { } + {7} |
| Coxeter diagram | |
| Symmetry group | D7h, [7,2], (*227), order 28 |
| Rotation group | D7, [7,2]+, (227), order 14 |
| Dual polyhedron | heptagonal prism |
| Face configuration | V4.4.7 |
| Properties | convex, face-transitive |
Related polyhedra
| Name | Digonal bipyramid | Triangular bipyramid (J12) | Square bipyramid (O) | Pentagonal bipyramid (J13) | Hexagonal bipyramid | Heptagonal bipyramid | Octagonal bipyramid | Enneagonal bipyramid | Decagonal bipyramid | ... | Apeirogonal bipyramid |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image |  |
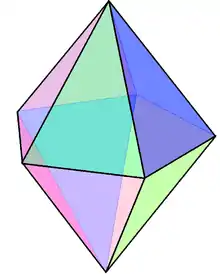 |
 |
 |
 |
 |
... | ||||
| Spherical tiling image |  |
 |
 |
 |
 |
 |
 |
Plane tiling image | |||
| Face configuration | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ... | V∞.4.4 |
| Coxeter diagram | ... |
References
- Heptagonal Dipyramid dmccooey.com [2014-6-23]
- Pugh, Anthony (1976), Polyhedra: A Visual Approach, University of California Press, pp. 21, 27, 62, ISBN 9780520030565.
External links
- Weisstein, Eric W. "Dipyramid". MathWorld.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML models <7>
- Conway Notation for Polyhedra Try: dP7
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.