Nonconvex great rhombicuboctahedron
In geometry, the nonconvex great rhombicuboctahedron is a nonconvex uniform polyhedron, indexed as U17. It has 26 faces (8 triangles and 18 squares), 48 edges, and 24 vertices.[1] It is represented by Schläfli symbol t0,2{4,3⁄2} and Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Its vertex figure is a crossed quadrilateral.
. Its vertex figure is a crossed quadrilateral.
| Nonconvex great rhombicuboctahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 26, E = 48 V = 24 (χ = 2) |
| Faces by sides | 8{3}+(6+12){4} |
| Wythoff symbol | 2 3 4/3 | 2 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U17, C59, W85 |
| Dual polyhedron | Great deltoidal icositetrahedron |
| Vertex figure |  4.4.4.3/2 |
| Bowers acronym | Querco |

This model shares the name with the convex great rhombicuboctahedron, also called the truncated cuboctahedron.
An alternate name for this figure is quasirhombicuboctahedron. From that derives its Bowers acronym: querco.
Orthogonal projections

Cartesian coordinates
Cartesian coordinates for the vertices of a nonconvex great rhombicuboctahedron centered at the origin with edge length 1 are all the permutations of
- (±ξ, ±1, ±1),
where ξ = √2 − 1.
Related polyhedra
It shares the vertex arrangement with the convex truncated cube. It additionally shares its edge arrangement with the great cubicuboctahedron (having the triangular faces and 6 square faces in common), and with the great rhombihexahedron (having 12 square faces in common). It has the same vertex figure as the pseudo great rhombicuboctahedron, which is not a uniform polyhedron.
 Truncated cube |
 Great rhombicuboctahedron |
 Great cubicuboctahedron |
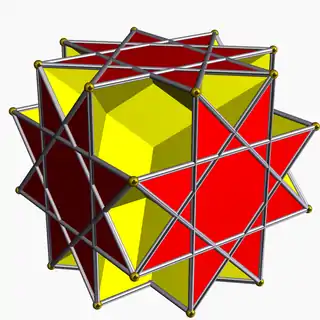 Great rhombihexahedron |
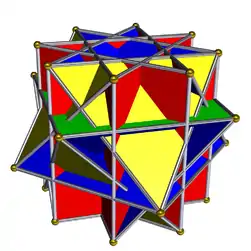 Pseudo great rhombicuboctahedron |
Great deltoidal icositetrahedron
| Great deltoidal icositetrahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 24, E = 48 V = 26 (χ = 2) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU17 |
| dual polyhedron | Nonconvex great rhombicuboctahedron |

The great deltoidal icositetrahedron is the dual of the nonconvex great rhombicuboctahedron.
References
- Maeder, Roman. "17: great rhombicuboctahedron". MathConsult.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208
External links
Weisstein, Eric W. "Great Deltoidal Icositetrahedron". MathWorld.
- Weisstein, Eric W. "Uniform great rhombicuboctahedron". MathWorld.
- Great Rhombicuboctahedron Paper model