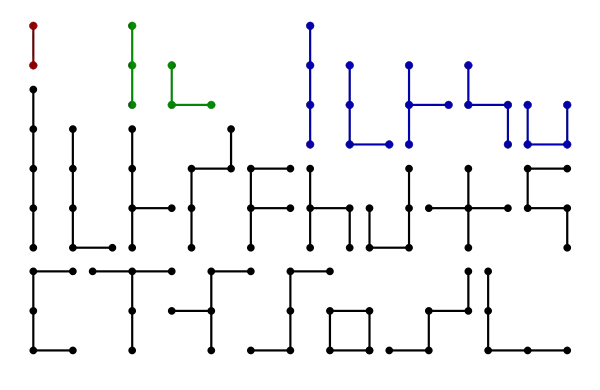
Polystick

In recreational mathematics, a polystick (or polyedge) is a polyform with a line segment (a 'stick') as the basic shape. A polystick is a connected set of segments in a regular grid. A square polystick is a connected subset of a regular square grid. A triangular polystick is a connected subset of a regular triangular grid. Polysticks are classified according to how many line segments they contain.[1]

When reflections are considered distinct we have the one-sided polysticks. When rotations and reflections are not considered to be distinct shapes, we have the free polysticks. Thus, for example, there are 7 one-sided square tristicks because two of the five shapes have left and right versions.[2][3]

Square Polysticks

SticksNameFreeOne-Sided
1monostick11
2distick22
3tristick57
4tetrastick1625
5pentastick5599
6hexastick222416
7heptastick9501854

Triangular Polysticks

SticksNameFree
1monostick1
2distick3
3tristick12
4tetrastick60
5pentastick375
6hexastick2613
7heptastick19074

The set of n-sticks that contain no closed loops is equivalent, with some duplications, to the set of (n+1)-ominos, as each vertex at the end of every line segment can be replaced with a single square of a polyomino. In general, an n-stick with m loops is equivalent to a (n−m+1)-omino (as each loop means that one line segment does not add a vertex to the figure).

Diagram
The free square polysticks of sizes 1 through 4, including 1 monostick (red), 2 disticks (green), 5 tristicks (blue), and 16 tetrasticks (black).

References
  1. OEIS: A019988OEIS: A159867OEIS: A197459
  2. Weisstein, Eric W. "Polystick." From MathWorld
  3. Counting polyforms, at the Solitaire Laboratory
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.