Rectified 120-cell

In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.

Four rectifications

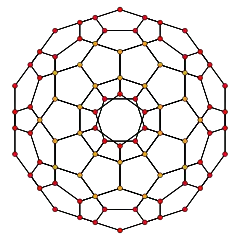120-cell
Rectified 120-cell

600-cell
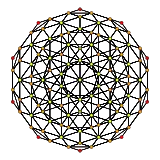Rectified 600-cell
Orthogonal projections in H3 Coxeter plane

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC120.

There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself. The birectified 120-cell is more easily seen as a rectified 600-cell, and the trirectified 120-cell is the same as the dual 600-cell.

Rectified 120-cell
Rectified 120-cell

Schlegel diagram, centered on icosidodecahedon, tetrahedral cells visible
TypeUniform 4-polytope
Uniform index33
Coxeter diagram
Schläfli symbolt1{5,3,3}
or r{5,3,3}
Cells720 total:
120 (3.5.3.5)
600 (3.3.3)
Faces3120 total:
2400 {3}, 720 {5}
Edges3600
Vertices1200
Vertex figure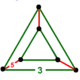
triangular prism
Symmetry groupH4 or [3,3,5]
Propertiesconvex, vertex-transitive, edge-transitive
Net

In geometry, the rectified 120-cell or rectified hecatonicosachoron is a convex uniform 4-polytope composed of 600 regular tetrahedra and 120 icosidodecahedra cells. Its vertex figure is a triangular prism, with three icosidodecahedra and two tetrahedra meeting at each vertex.

Alternative names:

  • Rectified 120-cell (Norman Johnson)
  • Rectified hecatonicosichoron / rectified dodecacontachoron / rectified polydodecahedron
  • Icosidodecahedral hexacosihecatonicosachoron
  • Rahi (Jonathan Bowers: for rectified hecatonicosachoron)
  • Ambohecatonicosachoron (Neil Sloane & John Horton Conway)

Projections
3D parallel projection
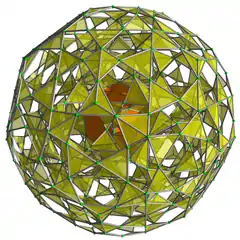Parallel projection of the rectified 120-cell into 3D, centered on an icosidodecahedral cell. Nearest cell to 4D viewpoint shown in orange, and tetrahedral cells shown in yellow. Remaining cells culled so that the structure of the projection is visible.
Orthographic projections by Coxeter planes
H4 - F4

[30]
[20]
[12]
H3 A2 / B3 / D4 A3 / B2

[10]
[6]
[4]

Notes

    References
    • Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
      • (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
      • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
      • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
    • J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
    • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
    Fundamental convex regular and uniform polytopes in dimensions 2–10
    Family An Bn I2(p) / Dn E6 / E7 / E8 / F4 / G2 Hn
    Regular polygon Triangle Square p-gon Hexagon Pentagon
    Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
    Uniform 4-polytope 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
    Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
    Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
    Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
    Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
    Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
    Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
    Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
    Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.