Strain partitioning

Strain partitioning is commonly referred to as a deformation process in which the total strain experienced on a rock, area, or region, is heterogeneously distributed in terms of the strain intensity and strain type (i.e. pure shear, simple shear, dilatation).[1][2][3] This process is observed on a range of scales spanning from the grain – crystal scale to the plate – lithospheric scale, and occurs in both the brittle and plastic deformation regimes.[1][2] The manner and intensity by which strain is distributed are controlled by a number of factors listed below.[2]

Influencing factors

All four of these factors below may individually or in combination contribute toward the distribution of strain. Therefore, each of these factors must be taken into consideration when analyzing how and why strain is partitioned:[2]

  1. Anisotropy such as preexisting structures, compositional layering, or cleavage planes. Isotropic lines "separate mutually orthogonal principle trajectories on each side. In a plane-strain field, the strain is zero at isotropic points and lines, and they can be termed neutral points and neutral lines."[4]
  2. Rheology
  3. Boundary conditions – The geometrical and mechanical properties
  4. Stress orientation – critical angles by which stress is applied[1][2][3]

Subdivisions

Strain partitioning across the literature is diverse and has been divided into three subdivisions according to the American Geological Institute.[5]

  1. Superposition of individual strain components that produce the finite strain[5]
  2. The accumulation of strain influenced by constituent rock materials[5]
  3. Individual deformation mechanisms that contribute toward producing the finite strain[5]

Superposition of individual strain components

The superposition of individual strain components can be expressed at the tectonic scale involving oblique convergent margins and transpression / transtension tectonic regimes.[1]

Oblique convergent margins
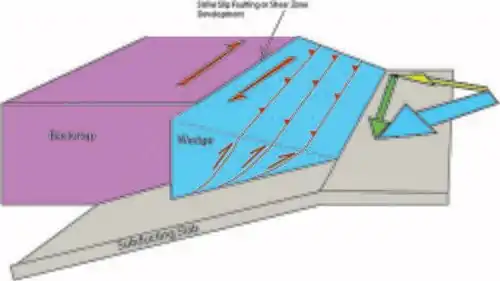
Block diagram illustrating strain partitioning at an oblique convergent margin. The obliquity of plate convergence (blue arrows) induces stress components that are normal to the margin (yellow arrow) and parallel to the margin (green arrow). Elevated magnitudes of the arc parallel component induces horizontal translation (red arrows) between the wedge and the backstop. Adapted and modified from Platt, 1993.[6]

Convergent margins where the angle of subduction is oblique will often result in the partitioning of strain into an arc parallel component (accommodated by strike slip faults or shear zones) and an arc normal component (accommodated through thrust faults).[6][7] This occurs as a response to shear stress exerted at the base of the overriding plate that is not perpendicular to the plate margin.[6][7][8]

Fundamental factors which control strain partitioning within oblique orogens
  • Stress Orientation:Subduction angle – Increased subduction angle increases arc parallel component[6][7]
  • Rheology and Anisotropy:Mechanical properties of the wedge: (Coulomb vs plastic) influences wedge geometry[6][7]
  • Boundary Conditions: Friction and geometry between the backstop and wedge[6][7]

Example: Himalayan Orogen

The Himalaya is a strain partitioned orogen which resulted from the oblique convergence between India and Asia.[9] Convergence between the two landmasses persists today at a rate of 2 cm/yr.[9] The obliquity of plate convergence increases toward the western portion of the orogen, thus inducing a greater magnitude of strain partitioning within the western Himalaya than in the central.[9]

The table below shows relative velocities of India's convergence with Asia. The lateral variability in velocity between the central and marginal regions of the orogen suggest strain is partitioned due to oblique convergence.[8][9]

LocationArc NormalArc Parallel
Western~10 mm/yr Northward~20 mm/yr Westward
Central~30 mm/yr Northward~0 mm/yr
Eastern~15 mm/yr Northward~20 mm/yr Eastward

Table reference:[8]

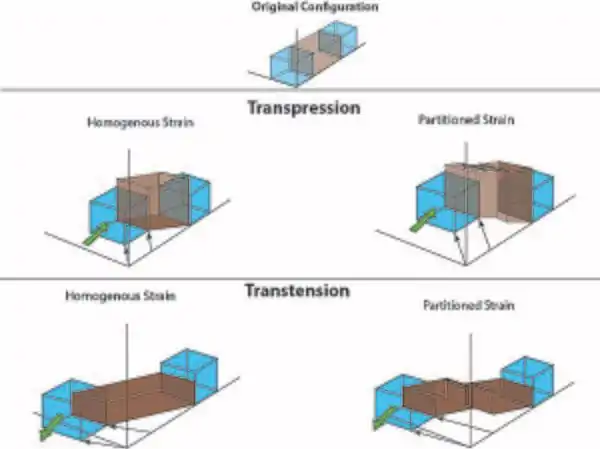
Transpression and transtension

Strain partitioning is common within transpressive and transtensive tectonic domains.[10][11] Both regimes involve a component of pure shear (transpression – compressive, transtension – extensive) and a component of simple shear.[3][10][11] Strain may be partitioned by the development of a strike slip fault or shear zone across the actively deforming region.[10][11]

Example: Coast Mountains British Columbia

The Coast Mountains of British Columbia are interpreted as a transpressive orogen which formed during the Cretaceous.[12] Oblique subduction induced the development of several shear zones which strike parallel to the orogen.[12] The presence of these shear zones suggest that strain is partitioned within the Coast Orogen which resulted in horizontal translation of terranes for several hundred kilometers parallel to the orogen.[12]

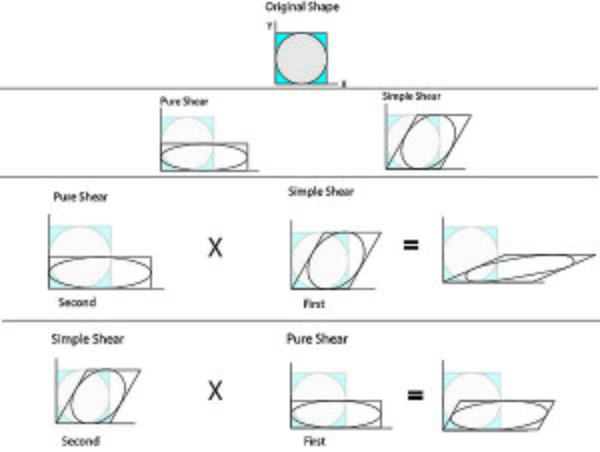
Block diagram illustrating the difference between homogeneous and partitioned strain within transpressive and transtensive tectonic regimes. The partitioning of strain occurs through the development of a strike slip or shear zone (shown with red arrows) across the actively deforming region (brown). Adaptation and modification from (Teyssier et al., 1995;[10] Fossen, 2012;[3] Jones and Tanner, 1995;[1] Sanderson and Marchini, 1984[13])

Strain factorization

Strain factorization is a mathematical approach to quantify and characterize the variation of strain components in terms of the intensity and distribution that produces the finite strain throughout a deformed region.[13][14][15][16] This effort is achieved through matrix multiplication.[14][15] Refer to the figure below to conceptually visualize what is obtained through strain factorization.

Conceptual illustration of strain factorization. This highlights how the order of superposition of pure and simple shear components produce differing geometries, as matrix multiplication is non-commutative. Adaptation and modifications from Ramsay and Huber, 1983;[14] Ramsay and Huber, 1987[15]

Influence of rock material rheology

At the grain and crystal scale, strain partitioning may occur between minerals (or clasts and matrix) governed by their rheological contrasts.[2][5][17][18] Constituent minerals of differing rheological properties in a rock will accumulate strain differently, thus inducing mechanically preferable structures and fabrics.[17][18]

Example

Rocks that contain incompetent (mechanically weak) minerals such as micas and more competent (mechanically stronger) minerals such as quartz or feldspars, may develop a shear band fabric.[17][18] The incompetent minerals will preferentially form the C-surfaces and competent minerals will form along the S-surfaces.[17][18]

Individual deformation mechanisms
Simplistic illustration of different deformation mechanisms which produce the finite strain. Citation for different types of deformation mechanisms acquired from (Passchier and Trouw, 2005)[19]

Strain partitioning is also known as a procedure for decomposing the overall strain into individual deformation mechanisms which allowed for strain to be accommodated.[14] This approach is performed from geometrical analysis of rocks on the grain – crystal scale.[14] Strain partitioning of deformation mechanisms incorporates those mechanisms which occur both simultaneously and/or subsequently as tectonic conditions evolve, as deformation mechanisms are a function of strain rate and pressure-temperature conditions.[14][16] Performing such a procedure is important for structural and tectonic analysis as it provides parameters and constraints for constructing deformation models.[16][20]

See also

References
  1. Jones, Richard; Tanner, P.W. Geoff (1995). "Strain partitioning in transpression zones". Journal of Structural Geology. 17 (6): 793–802. Bibcode:1995JSG....17..793J. doi:10.1016/0191-8141(94)00102-6.
  2. Carreras, Jordi; Cosgrove, John; Druguet, Elena (2013). "Strain partitioning in banded and/or anisotropic rocks: Implications for inferring tectonic regimes". Journal of Structural Geology. 50: 7–21. Bibcode:2013JSG....50....7C. doi:10.1016/j.jsg.2012.12.003.
  3. Fossen, Haakon (2012). Structural Geology. New York, USA: Cambridge University Press. ISBN 978-0-521-51664-8.
  4. Jean-Pierre Brun (1983) "Isotropic points and lines in strain fields", Journal of Structural Geology 5(3):321–7
  5. Neuendorf, Kaus; Mehl, James; Jackson, Julia (2005). Glossary of Geology (5 ed.). Alexandria, VA, United States: American Geological Institute. ISBN 978-0-922152-76-6.
  6. Platt, J.P. (1993). "Mechanics of Oblique Convergence". Journal of Geophysical Research. 98 (B9): 16, 239–16, 256. Bibcode:1993JGR....9816239P. doi:10.1029/93JB00888.
  7. McCaffrey, Robert (1992). "Oblique Plate Convergence, Slip Vectors, and Forearc Deformation". Journal of Geophysical Research. 97 (B6): 8905–8915. Bibcode:1992JGR....97.8905M. doi:10.1029/92JB00483.
  8. Syron, Richard; Taylor, Michaeal; Murphy, Michael (2011). "Oblique convergence, arc-parallel extension, and the role of strike-slip faulting in the High Himalaya". Geosphere. 7 (2): 582–596. Bibcode:2011Geosp...7..582S. doi:10.1130/GES00606.1.
  9. Murphy, M.A.; Taylor, M.H.; Gosse, J.; Silver, R.P.; Whipp, D.M.; Beaumont, C. (2014). "Limit of strain partitioning in the Himalaya marked by large earthquakes in western Nepal". Nature Geoscience. 7 (1): 38–42. Bibcode:2014NatGe...7...38M. doi:10.1038/NGEO2017.
  10. Teyssier, Christian; Tikoff, Basil; Markley, Michelle (1995). "Oblique plate motion and continental tectonics". Geology. 23 (5): 447. Bibcode:1995Geo....23..447T. doi:10.1130/0091-7613(1995)023<0447:OPMACT>2.3.CO;2.
  11. Fossen, Haakon; Tikoff, Basil; Teyssier, Christian (1994). "Strain modeling of transpressional and transtensional deformation" (PDF). Norsk Geologisk Tidsskrift. 74: 134–145.
  12. Chardon, Dominique; Andronicos, Christopher; Hollister, Lincoln (1999). "Large-scale transpressive shear zone patterns and displacements within magmatic arcs: The Coast Plutonic Complex, British Columbia". Tectonics. 18 (2): 278–292. Bibcode:1999Tecto..18..278C. doi:10.1029/1998TC900035.
  13. Sanderson, David; Marchini, W.R.D. (1984). "Transpression". Journal of Structural Geology. 6 (5): 449–458. Bibcode:1984JSG.....6..449S. doi:10.1016/0191-8141(84)90058-0.
  14. Ramsay, John; Huber, Martin (1983). The Techniques of Modern Structural Geology Volume 1: Strain Analysis. London: Academic Press. ISBN 978-0-12-576901-3.
  15. Ramsay, John; Huber, Martin (1987). The Techniques of Modern Structural Geology Volume 2: Folds and Fractures. London: Academic Press. ISBN 978-0-12-576902-0.
  16. Evans, Mark; Dunne, William (1991). "Strain factorization and partitioning in the North Mountain thrust sheet, central Appalachians, U.S.A". Journal of Structural Geology. 13 (1): 21–35. Bibcode:1991JSG....13...21E. doi:10.1016/0191-8141(91)90098-4.
  17. Goodwin, Laurel; Tikoff, Basil (2002). "Competency contrast, kinematics, and the development of foliations and lineations in the crust". Journal of Structural Geology. 24 (6–7): 1065–1085. Bibcode:2002JSG....24.1065G. doi:10.1016/S0191-8141(01)00092-X.
  18. Michibayashi, Katsuyoshi; Murakami, Masami (2007). "Development of a shear band cleavage as a result of strain partitioning". Journal of Structural Geology. 29 (6): 1070–1082. Bibcode:2007JSG....29.1070M. doi:10.1016/j.jsg.2007.02.003. hdl:10297/508.
  19. Passchier, Cees; Trouw, Rudolph (2005). Micro-tectonics (5th ed.). New York: Springer. ISBN 978-3-540-64003-5.
  20. Mitra, Shankar (1976). "A Quantitative Study of Deformation Mechanisms and Finite Strain in Quartzites". Contributions to Mineralogy and Petrology. 59 (2): 203–226. Bibcode:1976CoMP...59..203M. doi:10.1007/BF00371309.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.