Tetraheptagonal tiling
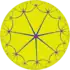
In geometry, the tetraheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of r{4,7}.
| Tetraheptagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (4.7)2 |
| Schläfli symbol | r{7,4} or rr{7,7} |
| Wythoff symbol | 7 4 7 7 | 2 |
| Coxeter diagram | |
| Symmetry group | [7,4], (*742) [7,7], (*772) |
| Dual | Order-7-4 rhombille tiling |
| Properties | Vertex-transitive edge-transitive |
Symmetry
 A half symmetry [1+,4,7] = [7,7] construction exists, which can be seen as two colors of heptagons. This coloring can be called a rhombiheptaheptagonal tiling. |
 The dual tiling is made of rhombic faces and has a face configuration V4.7.4.7. |
Related polyhedra and tiling
| *n42 symmetry mutations of quasiregular tilings: (4.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *4n2 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracompact | Noncompact | |||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[ni,4] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
|
| Config. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.ni)2 |
| Uniform heptagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,4], (*742) | [7,4]+, (742) | [7+,4], (7*2) | [7,4,1+], (*772) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| {7,4} | t{7,4} | r{7,4} | 2t{7,4}=t{4,7} | 2r{7,4}={4,7} | rr{7,4} | tr{7,4} | sr{7,4} | s{7,4} | h{4,7} | ||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V74 | V4.14.14 | V4.7.4.7 | V7.8.8 | V47 | V4.4.7.4 | V4.8.14 | V3.3.4.3.7 | V3.3.7.3.7 | V77 | ||
| Uniform heptaheptagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,7], (*772) | [7,7]+, (772) | ||||||||||
= |
= |
= |
= |
= |
= |
= |
= | ||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {7,7} | t{7,7} |
r{7,7} | 2t{7,7}=t{7,7} | 2r{7,7}={7,7} | rr{7,7} | tr{7,7} | sr{7,7} | ||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
|||||
| V77 | V7.14.14 | V7.7.7.7 | V7.14.14 | V77 | V4.7.4.7 | V4.14.14 | V3.3.7.3.7 | ||||
| Dimensional family of quasiregular polyhedra and tilings: 7.n.7.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *7n2 [n,7] |
Hyperbolic... | Paracompact | Noncompact | ||||||||
| *732 [3,7] |
*742 [4,7] |
*752 [5,7] |
*762 [6,7] |
*772 [7,7] |
*872 [8,7]... |
*∞72 [∞,7] |
[iπ/λ,7] | ||||
| Coxeter | |||||||||||
| Quasiregular figures configuration |
 3.7.3.7 |
 4.7.4.7 |
 7.5.7.5 |
 7.6.7.6 |
 7.7.7.7 |
 7.8.7.8 |
 7.∞.7.∞ |
7.∞.7.∞ | |||
See also
| Wikimedia Commons has media related to Uniform tiling 4-7-4-7. |
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

