Heptagrammic cupola
In geometry, the heptagrammic cupola is a star-cupola made from a heptagram, {7/3} and parallel tetradecagram, {14/3}, connected by 7 mutually intersecting equilateral triangles and squares.
| Heptagrammic cupola | |
|---|---|
 | |
| Type | Star-cupola |
| Faces | 7 triangles 7 squares 1 {7/3} 1 {14/3} |
| Edges | 35 |
| Vertices | 21 |
| Schläfli symbol | {7/3} || t{7/3} |
| Symmetry group | C7v, [7], (*77) |
| Rotation group | C7, [7]+, (77) |
| Dual polyhedron | - |
Related polyhedra
| n / d | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 | 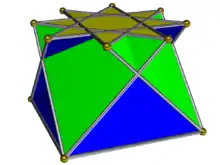 {4/3} |
 {5/3} |
 {7/3} |
 {8/3} |
| 5 | — | — |  {7/5} |
 {8/5} |
Crossed heptagrammic cupola
| Crossed heptagrammic cupola | |
|---|---|
 | |
| Type | Star-cupola |
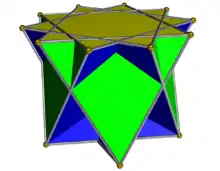
| Faces | 7 triangles 7 squares 1 {7/5} 1 {14/5} |
| Edges | 35 |
| Vertices | 21 |
| Schläfli symbol | {7/5} || t{7/5} |
| Symmetry group | C7v, [7], (*77) |
| Rotation group | C7, [7]+, (77) |
| Dual polyhedron | - |
The crossed heptagrammic cupola is a star-cupola made from a heptagram, {7/5} and parallel tetradecagram, {14/5}, connected by 7 mutually intersecting equilateral triangles and squares.
References
- Jim McNeill, Cupola OR Semicupola
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.