Pentagonal hexecontahedron

In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images (or "enantiomorphs") of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.

Pentagonal hexecontahedron
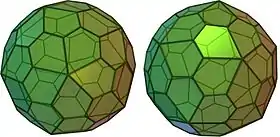(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	gD
Face type	V3.3.3.3.5 irregular pentagon
Faces	60
Edges	150
Vertices	92
Vertices by type	12 {5} 20+60 {3}
Symmetry group	I, 1/2H3, [5,3]^+, (532)
Rotation group	I, [5,3]^+, (532)
Dihedral angle	153°10′43″
Properties	convex, face-transitive chiral
Snub dodecahedron (dual polyhedron)	Net

3D model of a pentagonal hexecontahedron

Construction

The pentagonal hexecontahedron can be constructed from a snub dodecahedron without taking the dual. Pentagonal pyramids are added to the 12 pentagonal faces of the snub dodecahedron, and triangular pyramids are added to the 20 triangular faces that do not share an edge with a pentagon. The pyramid heights are adjusted to make them coplanar with the other 60 triangular faces of the snub dodecahedron. The result is the pentagonal hexecontahedron.[1]

Geometry

The faces are irregular pentagons with two long edges and three short edges. Let ${\displaystyle \xi \approx 0.943\,151\,259\,24}$ be the real zero of the polynomial ${\displaystyle x^{3}+2x^{2}-\phi ^{2}}$, where ${\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}}$ is the golden ratio. Then the ratio ${\displaystyle l}$ of the edge lengths is given by:

${\displaystyle l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74}$.

The faces have four equal obtuse angles and one acute angle (between the two long edges). The obtuse angles equal ${\displaystyle \arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }}$, and the acute one equals ${\displaystyle \arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }}$. The dihedral angle equals ${\displaystyle \arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }}$. Note that the face centers of the snub dodecahedron cannot serve directly as vertices of the pentagonal hexecontahedron: the four triangle centers lie in one plane but the pentagon center does not; it needs to be radially pushed out to make it coplanar with the triangle centers. Consequently, the vertices of the pentagonal hexecontahedron do not all lie on the same sphere and by definition it is not a zonohedron.

To find the volume and surface area of a pentagonal hexecontahedron, denote the longer side of one of the pentagonal faces as ${\displaystyle b}$, and set a constant t[2]${\displaystyle t={\frac {{\sqrt[{3}]{44+12\phi (9+{\sqrt {81\phi -15}})}}+{\sqrt[{3}]{44+12\phi (9-{\sqrt {81\phi -15}})}}-4}{12}}\approx 0.471\,575\,629\,622}$ .

Then the surface area (A) is:

${\displaystyle A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}}$.

And the volume (V) is:

${\displaystyle V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}}$.

Variations

Isohedral variations can be constructed with pentagonal faces with 3 edge lengths.

This variation shown can be constructed by adding pyramids to 12 pentagonal faces and 20 triangular faces of a snub dodecahedron such that the new triangular faces are coparallel to other triangles and can be merged into the pentagon faces.

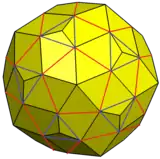Snub dodecahedron with augmented pyramids and merged faces

Example variation

Net

Orthogonal projections

The pentagonal hexecontahedron has three symmetry positions, two on vertices, and one mid-edge.

Orthogonal projections

Projective symmetry	[3]	[5]^+	[2]
Image
Dual image

Related polyhedra and tilings

Spherical pentagonal hexecontahedron

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)							[5,3]^+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

This polyhedron is topologically related as a part of sequence of polyhedra and tilings of pentagons with face configurations (V3.3.3.3.n). (The sequence progresses into tilings the hyperbolic plane to any n.) These face-transitive figures have (n32) rotational symmetry.

n32 symmetry mutations of snub tilings: 3.3.3.3.n
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

See also

• Truncated pentagonal hexecontahedron
• Amazon Spheres

References

1. Reference
2. "Pentagonal Hexecontahedron - Geometry Calculator". rechneronline.de. Retrieved 2020-05-26.

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 29, Pentagonal hexecontahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal hexecontahedron )

External links

• Eric W. Weisstein, Pentagonal hexecontahedron (Catalan solid) at MathWorld.
• Pentagonal Hexecontrahedron – Interactive Polyhedron Model