Quantum eraser experiment
| Part of a series on |
| Quantum mechanics |
|---|
In quantum mechanics, the quantum eraser experiment is an interferometer experiment that demonstrates several fundamental aspects of quantum mechanics, including quantum entanglement and complementarity. [1] [2] [3] The quantum eraser experiment is a variation of Thomas Young's classic double-slit experiment. It establishes that when action is taken to determine which of 2 slits a photon has passed through, the photon cannot interfere with itself. When a stream of photons is marked in this way, then the interference fringes characteristic of the Young experiment will not be seen. The experiment also creates situations in which a photon that has been "marked" to reveal through which slit it has passed can later be "unmarked." A photon that has been "marked" cannot interfere with itself and will not produce fringe patterns, but a photon that has been "marked" and then "unmarked" will interfere with itself and produce the fringes characteristic of Young's experiment.[1]
The experiment
This experiment involves an apparatus with two main sections. After two entangled photons are created, each is directed into its own section of the apparatus. Anything done to learn the path of the entangled partner of the photon being examined in the double-slit part of the apparatus will influence the second photon, and vice versa. The advantage of manipulating the entangled partners of the photons in the double-slit part of the experimental apparatus is that experimenters can destroy or restore the interference pattern in the latter without changing anything in that part of the apparatus. Experimenters do so by manipulating the entangled photon, and they can do so before or after its partner has passed through the slits and other elements of experimental apparatus between the photon emitter and the detection screen. Under conditions where the double-slit part of the experiment has been set up to prevent the appearance of interference phenomena (because there is definitive "which path" information present), the quantum eraser can be used to effectively erase that information. In doing so, the experimenter restores interference without altering the double-slit part of the experimental apparatus.[1]
A variation of this experiment, delayed choice quantum eraser, allows the decision whether to measure or destroy the "which path" information to be delayed until after the entangled particle partner (the one going through the slits) has either interfered with itself or not.[4] In delayed-choice experiments quantum effects can mimic an influence of future actions on past events. However, the temporal order of measurement actions is not relevant. [5]
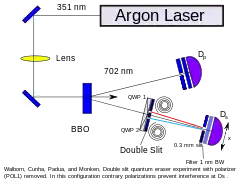
First, a photon is shot through a specialized nonlinear optical device: a beta barium borate (BBO) crystal. This crystal converts the single photon into two entangled photons of lower frequency, a process known as spontaneous parametric down-conversion (SPDC). These entangled photons follow separate paths. One photon goes directly to a polarization-resolving detector, while the second photon passes through the double-slit mask to a second polarization-resolving detector. Both detectors are connected to a coincidence circuit, ensuring that only entangled photon pairs are counted. A stepper motor moves the second detector to scan across the target area, producing an intensity map. This configuration yields the familiar interference pattern.

Next, a circular polarizer is placed in front of each slit in the double-slit mask, producing clockwise circular polarization in light passing through one slit, and counter-clockwise circular polarization in the other slit (see Figure 1). (Which slit corresponds to which polarization depends on the polarization reported by the first detector.) This polarization is measured at the second detector, thus "marking" the photons and destroying the interference pattern (see Fresnel–Arago laws).
Finally, a linear polarizer is introduced in the path of the first photon of the entangled pair, giving this photon a diagonal polarization (see Figure 2). Entanglement ensures a complementary diagonal polarization in its partner, which passes through the double-slit mask. This alters the effect of the circular polarizers: each will produce a mix of clockwise and counter-clockwise polarized light. Thus the second detector can no longer determine which path was taken, and the interference fringes are restored.
A double slit with rotating polarizers can also be accounted for by considering the light to be a classical wave.[6] However this experiment uses entangled photons, which are not compatible with classical mechanics.
Other applications
Quantum erasure technology can be used to increase the resolution of advanced microscopes.[7]
Common misconception
A very common misunderstanding about this experiment is that it may be used to instantaneously communicate information between two detectors. It is important to understand the role of the coincidence detector in this experimental setup. The linear polarizer in the top path is effectively filtering out half the entangled photons, and via the coincidence detector, is filtering out the corresponding photons in the bottom path. The coincidence detector can only function by comparing data from both sensors, making it impossible to use this setup for instant communication.
In other words, only a small percentage of the light passing through the BBO crystal is split into entangled pairs. The vast majority of photons passing through the crystal are not split, and must be removed from the final data set as unwanted noise. Since there is no way for the detectors to measure whether or not a photon had been part of an entangled pair, that decision is made by looking at the timing, and filtering out any photons that are not picked up at the same time as their 'twin' at the other detector. Thus, when a pair of entangled photons is created, but one of the two is blocked by a polarizer and lost, the remaining photon will be filtered out of the data set as if it was one of the many non-entangled photons. When viewed this way, it is not surprising that making changes to the upper path can have an impact to measurements taken on the lower path, as the two measurements are being compared and used to filter the data.
Note that in the final state of this experimental setup, measurements on the lower path always show a smeared out pattern on the raw data. Seeing an interference pattern is only possible by filtering the data with the coincidence detector and only looking at photons that were 1/2 of an entangled pair.
References
- Walborn, S. P.; et al. (2002). "Double-Slit Quantum Eraser". Phys. Rev. A. 65 (3): 033818. arXiv:quant-ph/0106078. Bibcode:2002PhRvA..65c3818W. doi:10.1103/PhysRevA.65.033818.
- Kastner (2019): 'Delayed Choice Quantum Eraser Neither Erases Nor Delays', Foundations of Physics
- Englert, Berthold-Georg (1999). "Remarks on Some Basic Issues in Quantum Mechanics" (PDF). Zeitschrift für Naturforschung. 54 (1): 11–32. Bibcode:1999ZNatA..54...11E. doi:10.1515/zna-1999-0104. Archived from the original (PDF) on 2017-08-09. Retrieved 2019-04-10.
- Yoon-Ho, Kim; Yu, R.; Kulik, S.P.; Shih, Y.H.; Scully, Marlan (2000). "A Delayed Choice Quantum Eraser". Physical Review Letters. 84 (1): 1–5. arXiv:quant-ph/9903047. Bibcode:2000PhRvL..84....1K. doi:10.1103/PhysRevLett.84.1. PMID 11015820.
- Ma, Xiao-song; Kofler, Johannes; Zeilinger, Anton (2016). "Delayed-choice gedanken experiments and their realizations". Rev. Mod. Phys. 88 (1): 015005. arXiv:1407.2930. Bibcode:2016RvMP...88a5005M. doi:10.1103/RevModPhys.88.015005.
- Chiao, R Y; Kwia, P G; Steinberg, A M (June 1995). "Quantum non-locality in two-photon experiments at Berkeley". Quantum and Semiclassical Optics: Journal of the European Optical Society Part B. 7 (3): 259–278. arXiv:quantph/9501016. Bibcode:1995QuSOp...7..259C. doi:10.1088/1355-5111/7/3/006.
- Aharonov, Yakir; Zubairy, M. Suhail (2005). "Time and the Quantum: Erasing the Past and Impacting the Future". Science. 307 (5711): 875–879. Bibcode:2005Sci...307..875A. CiteSeerX 10.1.1.110.2955. doi:10.1126/science.1107787. PMID 15705840.