ARGUS distribution

In physics, the ARGUS distribution, named after the particle physics experiment ARGUS,[1] is the probability distribution of the reconstructed invariant mass of a decayed particle candidate in continuum background.

ARGUS

Probability density function 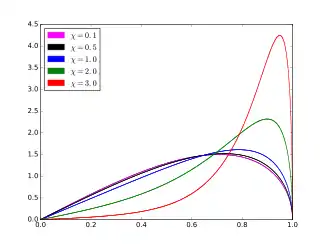c = 1.
Cumulative distribution function 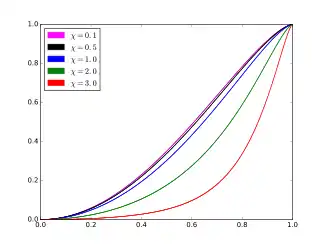c = 1.
Parameters	${\displaystyle c>0}$ cut-off (real) ${\displaystyle \chi >0}$ curvature (real)
Support	${\displaystyle x\in (0,c)\!}$
PDF	see text
CDF	see text
Mean	${\displaystyle \mu =c{\sqrt {\pi /8}}\;{\frac {\chi e^{-{\frac {\chi ^{2}}{4}}}I_{1}({\tfrac {\chi ^{2}}{4}})}{\Psi (\chi )}}}$ where I1 is the Modified Bessel function of the first kind of order 1, and ${\displaystyle \Psi (x)}$ is given in the text.
Mode	${\displaystyle {\frac {c}{{\sqrt {2}}\chi }}{\sqrt {(\chi ^{2}-2)+{\sqrt {\chi ^{4}+4}}}}}$
Variance	${\displaystyle c^{2}\!\left(1-{\frac {3}{\chi ^{2}}}+{\frac {\chi \phi (\chi )}{\Psi (\chi )}}\right)-\mu ^{2}}$

Definition

The probability density function (pdf) of the ARGUS distribution is:

${\displaystyle f(x;\chi ,c)={\frac {\chi ^{3}}{{\sqrt {2\pi }}\,\Psi (\chi )}}\cdot {\frac {x}{c^{2}}}{\sqrt {1-{\frac {x^{2}}{c^{2}}}}}\exp {\bigg \{}-{\frac {1}{2}}\chi ^{2}{\Big (}1-{\frac {x^{2}}{c^{2}}}{\Big )}{\bigg \}},}$

for ${\displaystyle 0\leq x<c}$. Here ${\displaystyle \chi }$ and ${\displaystyle c}$ are parameters of the distribution and

${\displaystyle \Psi (\chi )=\Phi (\chi )-\chi \phi (\chi )-{\tfrac {1}{2}},}$

where ${\displaystyle \Phi (x)}$ and ${\displaystyle \phi (x)}$ are the cumulative distribution and probability density functions of the standard normal distribution, respectively.

Cumulative distribution function

The cumulative distribution function (cdf) of the ARGUS distribution is

${\displaystyle F(x)=1-{\frac {\Psi \left(\chi {\sqrt {1-x^{2}/c^{2}}}\right)}{\Psi (\chi )}}}$.

Parameter estimation

Parameter c is assumed to be known (the kinematic limit of the invariant mass distribution), whereas χ can be estimated from the sample X₁, …, X_n using the maximum likelihood approach. The estimator is a function of sample second moment, and is given as a solution to the non-linear equation

${\displaystyle 1-{\frac {3}{\chi ^{2}}}+{\frac {\chi \phi (\chi )}{\Psi (\chi )}}={\frac {1}{n}}\sum _{i=1}^{n}{\frac {x_{i}^{2}}{c^{2}}}}$.

The solution exists and is unique, provided that the right-hand side is greater than 0.4; the resulting estimator ${\displaystyle \scriptstyle {\hat {\chi }}}$ is consistent and asymptotically normal.

Generalized ARGUS distribution

Sometimes a more general form is used to describe a more peaking-like distribution:

${\displaystyle f(x)={\frac {2^{-p}\chi ^{2(p+1)}}{\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2}}\chi ^{2})}}\cdot {\frac {x}{c^{2}}}\left(1-{\frac {x^{2}}{c^{2}}}\right)^{p}\exp \left\{-{\frac {1}{2}}\chi ^{2}\left(1-{\frac {x^{2}}{c^{2}}}\right)\right\},\qquad 0\leq x\leq c,\qquad c>0,\,\chi >0,\,p>-1}$

${\displaystyle F(x)={\frac {\Gamma \left(p+1,\,{\tfrac {1}{2}}\chi ^{2}\left(1-{\frac {x^{2}}{c^{2}}}\right)\right)-\Gamma (p+1,\,{\tfrac {1}{2}}\chi ^{2})}{\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2}}\chi ^{2})}},\qquad 0\leq x\leq c,\qquad c>0,\,\chi >0,\,p>-1}$

where Γ(·) is the gamma function, and Γ(·,·) is the upper incomplete gamma function.

Here parameters c, χ, p represent the cutoff, curvature, and power respectively.

The mode is:

${\displaystyle {\frac {c}{{\sqrt {2}}\chi }}{\sqrt {(\chi ^{2}-2p-1)+{\sqrt {\chi ^{2}(\chi ^{2}-4p+2)+(1+2p)^{2}}}}}}$

The mean is:

${\displaystyle \mu =c\,p\,{\sqrt {\pi }}{\frac {\Gamma (p)}{\Gamma ({\tfrac {5}{2}}+p)}}{\frac {\chi ^{2p+2}}{2^{p+2}}}{\frac {M\left(p+1,{\tfrac {5}{2}}+p,-{\tfrac {\chi ^{2}}{2}}\right)}{\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2}}\chi ^{2})}}}$

where M(·,·,·) is the Kummer's confluent hypergeometric function.[2]

The variance is:

${\displaystyle \sigma ^{2}=c^{2}{\frac {\left({\frac {\chi }{2}}\right)^{p+1}\chi ^{p+3}e^{-{\tfrac {\chi ^{2}}{2}}}+\left(\chi ^{2}-2(p+1)\right)\left\{\Gamma (p+2)-\Gamma (p+2,\,{\tfrac {1}{2}}\chi ^{2})\right\}}{\chi ^{2}(p+1)\left(\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2}}\chi ^{2})\right)}}-\mu ^{2}}$

p = 0.5 gives a regular ARGUS, listed above.

References

1. Albrecht, H. (1990). "Search for hadronic b→u decays". Physics Letters B. 241 (2): 278–282. Bibcode:1990PhLB..241..278A. doi:10.1016/0370-2693(90)91293-K. (More formally by the ARGUS Collaboration, H. Albrecht et al.) In this paper, the function has been defined with parameter c representing the beam energy and parameter p set to 0.5. The normalization and the parameter χ have been obtained from data.
2. Confluent hypergeometric function

Further reading

• Albrecht, H. (1994). "Measurement of the polarization in the decay B → J/ψK*". Physics Letters B. 340 (3): 217–220. Bibcode:1994PhLB..340..217A. doi:10.1016/0370-2693(94)01302-0.
• Pedlar, T.; Cronin-Hennessy, D.; Hietala, J.; Dobbs, S.; Metreveli, Z.; Seth, K.; Tomaradze, A.; Xiao, T.; Martin, L. (2011). "Observation of the h_c(1P) Using e⁺e⁻ Collisions above the DD Threshold". Physical Review Letters. 107 (4): 041803. arXiv:1104.2025. Bibcode:2011PhRvL.107d1803P. doi:10.1103/PhysRevLett.107.041803. PMID 21866994. S2CID 33751212.
• Lees, J. P.; Poireau, V.; Prencipe, E.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Martinelli, M.; Palano, A.; Pappagallo, M.; Eigen, G.; Stugu, B.; Sun, L.; Battaglia, M.; Brown, D. N.; Hooberman, B.; Kerth, L. T.; Kolomensky, Y. G.; Lynch, G.; Osipenkov, I. L.; Tanabe, T.; Hawkes, C. M.; Soni, N.; Watson, A. T.; Koch, H.; Schroeder, T.; Asgeirsson, D. J.; Hearty, C.; Mattison, T. S.; McKenna, J. A.; et al. (2010). "Search for Charged Lepton Flavor Violation in Narrow Υ Decays". Physical Review Letters. 104 (15): 151802. arXiv:1001.1883. Bibcode:2010PhRvL.104o1802L. doi:10.1103/PhysRevLett.104.151802. PMID 20481982. S2CID 14992286.