Asymmetric Laplace distribution
In probability theory and statistics, the asymmetric Laplace distribution (ALD) is a continuous probability distribution which is a generalization of the Laplace distribution. Just as the Laplace distribution consists of two exponential distributions of equal scale back-to-back about x = m, the asymmetric Laplace consists of two exponential distributions of unequal scale back to back about x = m, adjusted to assure continuity and normalization. The difference of two variates exponentially distributed with different means and rate parameters will be distributed according to the ALD. When the two rate parameters are equal, the difference will be distributed according to the Laplace distribution.
|
Probability density function 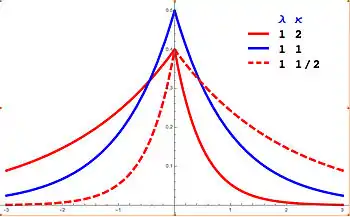 Asymmetric Laplace PDF with m = 0 in red. Note that the κ = 2 and 1/2 curves are mirror images. The κ = 1 curve in blue is the symmetric Laplace distribution. | |||
|
Cumulative distribution function 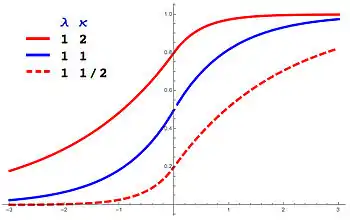 Asymmetric Laplace CDF with m = 0 in red. | |||
| Parameters | asymmetry (real) | ||
|---|---|---|---|
| Support | |||
| (see article) | |||
| CDF | (see article) | ||
| Mean | |||
| Median |
if if | ||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| CF | |||
Characterization
Probability density function
A random variable has an asymmetric Laplace(m, λ, κ) distribution if its probability density function is[1][2]
where s=sgn(x-m), or alternatively:
Here, m is a location parameter, λ > 0 is a scale parameter, and κ is an asymmetry parameter. When κ = 1, (x-m)s κs simplifies to |x-m| and the distribution simplifies to the Laplace distribution.
Characteristic function
The ALD characteristic function is given by:
For m = 0, the ALD is a member of the family of geometric stable distributions with α = 2. It follows that if and are two distinct ALD characteristic functions with m = 0, then
is also an ALD characteristic function with location parameter . The new scale parameter λ obeys
and the new skewness parameter κ obeys:
Moments, mean, variance, skewness
The n-th moment of the ALD about m is given by
From the binomial theorem, the n-th moment about zero (for m not zero) is then:
where is the generalized exponential integral function
The first moment about zero is the mean:
The variance is:
and the skewness is:
Generating asymmetric Laplace variates
Asymmetric Laplace variates (X) may be generated from a random variate U drawn from the uniform distribution in the interval (-κ,1/κ) by:
where s=sgn(U).
They may also be generated as the difference of two exponential distributions. If X1 is drawn from exponential distribution with mean and rate (m1,λ/κ) and X2 is drawn from an exponential distribution with mean and rate (m2,λκ) then X1 - X2 is distributed according to the asymmetric Laplace distribution with parameters (m1-m2, λ, κ)
Entropy
The differential entropy of the ALD is
The ALD has the maximum entropy of all distributions with a fixed value (1/λ) of where .
Alternative parametrization
An alternative parametrization is made possible by the characteristic function:
where is a location parameter, is a scale parameter, is an asymmetry parameter. This is specified in Section 2.6.1 and Section 3.1 of Lihn (2015). [3] Its probability density function is
where and . It follows that .
The n-th moment about is given by
The mean about zero is:
The variance is:
The skewness is:
The excess kurtosis is:
For small , the skewness is about . Thus represents skewness in an almost direct way.
References
- Kozubowski, Tomasz J.; Podgorski, Krzysztof (2000). "A Multivariate and Asymmetric Generalization of Laplace Distribution". Computational Statistics. 15 (4): 531. doi:10.1007/PL00022717. S2CID 124839639. Retrieved 2015-12-29.
- Jammalamadaka, S. Rao; Kozubowski, Tomasz J. (2004). "New Families of Wrapped Distributions for Modeling Skew Circular Data" (PDF). Communications in Statistics – Theory and Methods. 33 (9): 2059–2074. doi:10.1081/STA-200026570. S2CID 17024930. Retrieved 2011-06-13.
- Lihn, Stephen H.-T. (2015). "The Special Elliptic Option Pricing Model and Volatility Smile". SSRN: 2707810. Retrieved 2017-09-05.