Bates distribution

In probability and statistics, the Bates distribution, named after Grace Bates, is a probability distribution of the mean of a number of statistically independent uniformly distributed random variables on the unit interval.[1] This distribution is sometimes confused[2] with the Irwin–Hall distribution, which is the distribution of the sum (not the mean) of n independent random variables uniformly distributed from 0 to 1. Thus, the two distributions are simply versions of each other as they only differ in scale.

Bates

Probability density function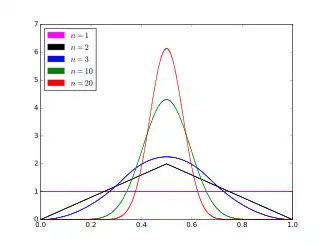
Cumulative distribution function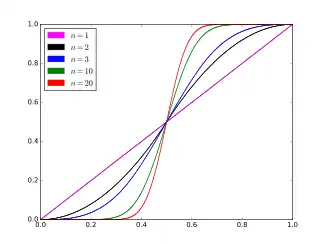
Parameters	${\displaystyle -\infty <a<b<\infty }$ ${\displaystyle n\geq 1}$ integer
Support	${\displaystyle x\in [a,b]}$
PDF	see below
Mean	${\displaystyle {\tfrac {1}{2}}(a+b)}$
Variance	${\displaystyle {\tfrac {1}{12n}}(b-a)^{2}}$
Skewness	0
Ex. kurtosis	${\displaystyle -{\tfrac {6}{5n}}}$
CF	${\displaystyle \left(-{\frac {in(e^{\tfrac {ibt}{n}}-e^{\tfrac {iat}{n}})}{(b-a)t}}\right)^{n}}$

Definition

The Bates distribution is the continuous probability distribution of the mean, X, of n independent uniformly distributed random variables on the unit interval, U_i:

${\displaystyle X={\frac {1}{n}}\sum _{k=1}^{n}U_{k}.}$

The equation defining the probability density function of a Bates distribution random variable X is

${\displaystyle f_{X}(x;n)={\frac {n}{2(n-1)!}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(nx-k)^{n-1}\operatorname {sgn}(nx-k)}$

for x in the interval (0,1), and zero elsewhere. Here sgn(nx − k) denotes the sign function:

${\displaystyle \operatorname {sgn}(nx-k)={\begin{cases}-1&nx<k\\0&nx=k\\1&nx>k.\end{cases}}}$

More generally, the mean of n independent uniformly distributed random variables on the interval [a,b]

${\displaystyle X_{(a,b)}={\frac {1}{n}}\sum _{k=1}^{n}U_{k}(a,b).}$

would have the probability density function (PDF) of

${\displaystyle g(x;n,a,b)=f_{X}\left({\frac {x-a}{b-a}};n\right){\text{ for }}a\leq x\leq b}$

Therefore, the PDF of the distribution is

${\displaystyle f(x)={\begin{cases}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\left({\frac {x-a}{b-a}}-k/n\right)^{n-1}\operatorname {sgn} \left({\frac {x-a}{b-a}}-k/n\right)&{\text{if }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}}$

Extensions to the Bates distribution

Instead of dividing by n we can also use √n to create a similar distribution with a constant variance (like unity). By subtracting the mean we can set the resulting mean to zero. This way the parameter n would become a purely shape-adjusting parameter, and we obtain a distribution which covers the uniform, the triangular and, in the limit, also the normal Gaussian distribution. By allowing also non-integer n a highly flexible distribution can be created (e.g. U(0,1) + 0.5U(0,1) gives a trapezoidal distribution). Actually the Student-t distribution provides a natural extension of the normal Gaussian distribution for modeling of long tail data. And such generalized Bates distribution is doing so for short tail data (kurtosis < 3).

The Bates distribution has an application to beamforming and pattern synthesis in reference [3]

See also

• Irwin–Hall distribution
• Normal distribution
• Central limit theorem
• Uniform distribution (continuous)
• Triangular distribution

Notes

1. Jonhson, N. L.; Kotz, S.; Balakrishnan (1995) Continuous Univariate Distributions, Volume 2, 2nd Edition, Wiley ISBN 0-471-58494-0(Section 26.9)
2. "The thing named "Irwin-Hall distribution" in d3.random is actually a Bates distribution · Issue #1647 · d3/d3". GitHub. Retrieved 2018-04-17.
3. https://ieeexplore.ieee.org/document/8299700/similar#similar

References

• Bates,G.E. (1955) "Joint distributions of time intervals for the occurrence of successive accidents in a generalized Polya urn scheme", Annals of Mathematical Statistics, 26, 705–720