Bootstrap aggregating
Bootstrap aggregating, also called bagging (from bootstrap aggregating), is a machine learning ensemble meta-algorithm designed to improve the stability and accuracy of machine learning algorithms used in statistical classification and regression. It also reduces variance and helps to avoid overfitting. Although it is usually applied to decision tree methods, it can be used with any type of method. Bagging is a special case of the model averaging approach.
| Part of a series on |
| Machine learning and data mining |
|---|
Description of the technique
Given a standard training set of size n, bagging generates m new training sets , each of size n′, by sampling from D uniformly and with replacement. By sampling with replacement, some observations may be repeated in each . If n′=n, then for large n the set is expected to have the fraction (1 - 1/e) (≈63.2%) of the unique examples of D, the rest being duplicates.[1] This kind of sample is known as a bootstrap sample. Sampling with replacement ensures each bootstrap is independent from its peers, as it does not depend on previous chosen samples when sampling. Then, m models are fitted using the above m bootstrap samples and combined by averaging the output (for regression) or voting (for classification).
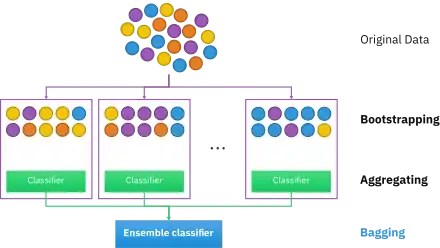
Bagging leads to "improvements for unstable procedures",[2] which include, for example, artificial neural networks, classification and regression trees, and subset selection in linear regression.[3] Bagging was shown to improve preimage learning.[4][5] On the other hand, it can mildly degrade the performance of stable methods such as K-nearest neighbors.[2]
Process of the Algorithm
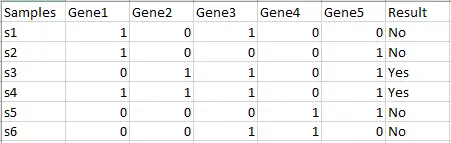
Original dataset
The original dataset contains several entries of samples from s1 to s5. Each sample has 5 features (Gene 1 to Gene 5). All samples are labeled as Yes or No for a classification problem.

Creation of Bootstrapped datasets
Given the table above to classify a new sample, first a bootstrapped dataset must be created using the data from the original dataset. This Bootstrapped dataset is typically the size of the original dataset, or smaller.
In this example, the size is 5 (s1 through s5). The Bootstrapped Dataset is created by randomly selecting samples from the original dataset. Repeat selections are allowed. Any samples that are not chosen for the bootstrapped dataset are placed in a separate dataset called the Out-of-Bag dataset.
See an example bootstrapped dataset below. It has 5 entries (same size as the original dataset). There are duplicated entries such as two s3 since the entries are selected randomly with replacement.

This step will repeat to generate m bootstrapped datasets.
Creating of Decision Trees

A Decision tree is created for each Bootstrapped dataset using randomly selected column values to split the nodes.
Predicting using Multiple Decision Trees
 When a new sample is added to the table. The bootstrapped dataset is used to determine the new entry's clasifier value.
When a new sample is added to the table. The bootstrapped dataset is used to determine the new entry's clasifier value.
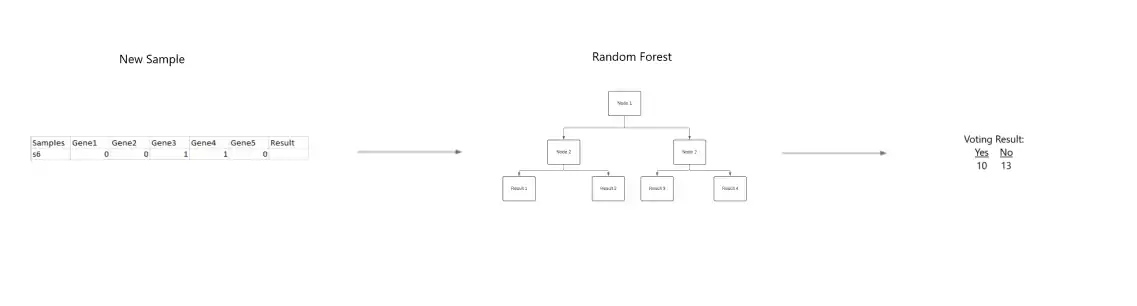
The new sample is tested in the random forest created by each bootstrapped dataset and each tree produces a classifier value for the new sample. For Classification, a process called voting is used to determine the final result, where the result produced the most frequently by the random forest is the given result for the sample. For Regression, the sample is assigned the average classifier value produced by the trees.
After the sample is tested in the random forest. A classifier value is assigned to the sample and it is added to the table.
Algorithm (Classification)
For Classification, use a training set , Inducer and the number of bootstrap samples as input. Generate a classifier as output[6]
- Create new training sets , from with replacement
- Classifier is built from each set using to determine the classification of set
- Finally classifier is generated by using the previously created set of classifiers on the original data set , the classification predicted most often by the sub-classifiers is the final classification
for i = 1 to m {
D' = bootstrap sample from D (sample with replacement)
Ci = I(D')
}
C*(x) = argmax Σ 1 (most often predicted label y)
y∈Y i:Ci(x)=y
Example: Ozone data
To illustrate the basic principles of bagging, below is an analysis on the relationship between ozone and temperature (data from Rousseeuw and Leroy (1986), analysis done in R).
The relationship between temperature and ozone appears to be nonlinear in this data set, based on the scatter plot. To mathematically describe this relationship, LOESS smoothers (with bandwidth 0.5) are used. Rather than building a single smoother for the complete data set, 100 bootstrap samples were drawn. Each sample is composed of a random subset of the original data and maintains a semblance of the master set’s distribution and variability. For each bootstrap sample, a LOESS smoother was fit. Predictions from these 100 smoothers were then made across the range of the data. The black lines represent these initial predictions. The lines lack agreement in their predictions and tend to overfit their data points: evident by the wobbly flow of the lines.

By taking the average of 100 smoothers, each corresponding to a subset of the original data set, we arrive at one bagged predictor (red line). The red line's flow is stable and does not overly conform to any data point(s).
Advantages vs Disadvantages
Advantages:
- Many weak learners aggregated typically outperform a single learner over the entire set, and has less overfit
- Removes variance in high-variance low-bias data sets[7]
- Can be performed in parallel, as each separate bootstrap can be processed on its own before combination[8]
Disadvantages:
- In a data set with high bias, bagging will also carry high bias into its aggregate[7]
- Loss of interpretability of a model.
- Can be computationally expensive depending on the data set
History
The concept of Bootstrap Aggregating is derived from the concept of Bootstrapping which was developed by Bradley Efron.[9] Bootstrap Aggregating was proposed by Leo Breiman who also coined the abbreviated term "Bagging" (Bootstrap aggregating). Breiman developed the concept of bagging in 1994 to improve classification by combining classifications of randomly generated training sets. He argued, “If perturbing the learning set can cause significant changes in the predictor constructed, then bagging can improve accuracy.”[3]
See also
References
- Aslam, Javed A.; Popa, Raluca A.; and Rivest, Ronald L. (2007); On Estimating the Size and Confidence of a Statistical Audit, Proceedings of the Electronic Voting Technology Workshop (EVT '07), Boston, MA, August 6, 2007. More generally, when drawing with replacement n′ values out of a set of n (different and equally likely), the expected number of unique draws is .
- Breiman, Leo (1996). "Bagging predictors". Machine Learning. 24 (2): 123–140. CiteSeerX 10.1.1.32.9399. doi:10.1007/BF00058655. S2CID 47328136.
- Breiman, Leo (September 1994). "Bagging Predictors" (PDF). Department of Statistics, University of California Berkeley. Technical Report No. 421. Retrieved 2019-07-28.
- Sahu, A., Runger, G., Apley, D., Image denoising with a multi-phase kernel principal component approach and an ensemble version, IEEE Applied Imagery Pattern Recognition Workshop, pp.1-7, 2011.
- Shinde, Amit, Anshuman Sahu, Daniel Apley, and George Runger. "Preimages for Variation Patterns from Kernel PCA and Bagging." IIE Transactions, Vol.46, Iss.5, 2014
- Bauer, Eric; Kohavi, Ron (1999). "An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants". Machine Learning. 36: 108–109. doi:10.1023/A:1007515423169. S2CID 1088806. Retrieved 6 December 2020.
- "What is Bagging (Bootstrap Aggregation)?". CFI. Corporate Finance Institute. Retrieved December 5, 2020.
- Zoghni, Raouf (September 5, 2020). "Bagging (Bootstrap Aggregating), Overview". Medium. The Startup.
- Efron, B. (1979). "Bootstrap methods: Another look at the jackknife". The Annals of Statistics. 7 (1): 1–26. doi:10.1214/aos/1176344552.
Further reading
- Breiman, Leo (1996). "Bagging predictors". Machine Learning. 24 (2): 123–140. CiteSeerX 10.1.1.32.9399. doi:10.1007/BF00058655. S2CID 47328136.
- Alfaro, E., Gámez, M. and García, N. (2012). "adabag: An R package for classification with AdaBoost.M1, AdaBoost-SAMME and Bagging". Cite journal requires
|journal=(help) - Kotsiantis, Sotiris (2014). "Bagging and boosting variants for handling classifications problems: a survey". Knowledge Eng. Review. 29 (1): 78–100. doi:10.1017/S0269888913000313.
- Boehmke, Bradley; Greenwell, Brandon (2019). "Bagging". Hands-On Machine Learning with R. Chapman & Hall. pp. 191–202. ISBN 978-1-138-49568-5.