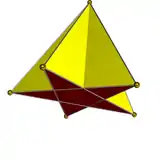
Pentagonal pyramid
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the vertex). Like any pyramid, it is self-dual.
| Pentagonal pyramid | |
|---|---|
 | |
| Type | Johnson J1 - J2 - J3 |
| Faces | 5 triangles 1 pentagon |
| Edges | 10 |
| Vertices | 6 |
| Vertex configuration | 5(32.5) (35) |
| Schläfli symbol | ( ) ∨ {5} |
| Symmetry group | C5v, [5], (*55) |
| Rotation group | C5, [5]+, (55) |
| Dual polyhedron | self |
| Properties | convex |
| Net | |
 | |

The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solids (J2).
It can be seen as the "lid" of an icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, J11
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Cartesian coordinates
The pentagonal pyramid can be seen as the "lid" of a regular icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, J11. From the Cartesian coordinates of the icosahedron, Cartesian coordinates for a pentagonal pyramid with edge length 2 may be inferred as
where τ (sometimes written as φ) is the golden ratio.[1]
The height H, from the midpoint of the pentagonal face to the apex, of a pentagonal pyramid with edge length a may therefore be computed as:
Its surface area A can be computed as the area of the pentagonal base plus five times the area of one triangle:
Its volume can be calculated as:
Related polyhedra
The pentagrammic star pyramid has the same vertex arrangement, but connected onto a pentagram base:
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | Octagonal | Enneagonal | Decagonal... |
| Improper | Regular | Equilateral | Isosceles | |||||
 |
 |
 |
 | |||||
 |
 |
 |
 |
 |
 |
 |
 | |
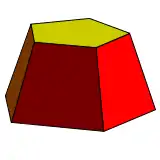 Pentagonal frustum is a pentagonal pyramid with its apex truncated |
 The top of an icosahedron is a pentagonal pyramid |
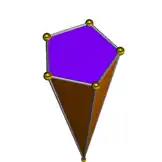
Dual polyhedron
The pentagonal pyramid is topologically a self-dual polyhedron. The dual edge lengths are different due to the polar reciprocation.
| Dual pentagonal pyramid | Net of dual |
|---|---|
 |
 |
Example

References
- Weisstein, Eric W. "Icosahedral Group". mathworld.wolfram.com. Retrieved 2020-04-12.
- Sapiña, R. "Area and volume of a pentagonal pyramid and Johnson solid J₂". Problemas y ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-06-29.
- Weisstein, Eric W. "Pentagonal Pyramid". mathworld.wolfram.com. Retrieved 2020-04-12.
External links
- Eric W. Weisstein, Pentagonal pyramid (Johnson solid) at MathWorld.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRML model)