Pentatope number

A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.

Derivation of pentatope numbers from a left-justified Pascal's triangle

The first few numbers of this kind are:

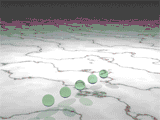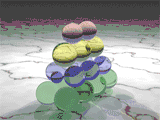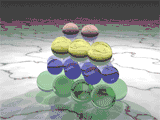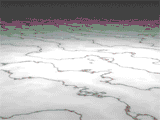
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365 (sequence A000332 in the OEIS)

A pentatope with side length 5 contains 70 3-spheres. Each layer represents one of the first five tetrahedral numbers. For example, the bottom (green) layer has 35 spheres in total.

Pentatope numbers belong to the class of figurate numbers, which can be represented as regular, discrete geometric patterns.[1]

Formula

The formula for the $n$ th pentatope number is represented by the 4th rising factorial of $n$ divided by the factorial of 4:

P_{n}={\frac {n^{\overline {4}}}{4!}}={\frac {n(n+1)(n+2)(n+3)}{24}}.

The pentatope numbers can also be represented as binomial coefficients:

P_{n}={\binom {n+3}{4}},

which is the number of distinct quadruples that can be selected from $n + 3$ objects, and it is read aloud as " $n$ plus three choose four".

Properties

Two of every three pentatope numbers are also pentagonal numbers. To be precise, the $(3 k - 2)$ th pentatope number is always the $(.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px;white-space:nowrap} 3 k 2 - k / 2)$ th pentagonal number and the $(3 k - 1)$ th pentatope number is always the $(3 k 2 + k / 2)$ th pentagonal number. The $(3 k)$ th pentatope number is the generalized pentagonal number obtained by taking the negative index $- 3 k 2 + k / 2$ in the formula for pentagonal numbers. (These expressions always give integers).[2]

The infinite sum of the reciprocals of all pentatope numbers is 4/3.[3] This can be derived using telescoping series.

\sum _{n=1}^{\infty }{\frac {4!}{n(n+1)(n+2)(n+3)}}={\frac {4}{3}}

Pentatope numbers can also be represented as the sum of the first $n$ tetrahedral numbers:[2]

P_{n}=\sum _{k=1}^{n}Te_{n}

Relation to single tetrahedral number:

P_{n}={\tfrac {1}{4}}(n+3)Te_{n},

No prime number is the predecessor of a pentatope number, and the largest semiprime which is the predecessor of a pentatope number is 1819.

Similarly, the only primes preceding a 6-simplex number are 83 and 461.

Test for pentatope numbers

We can derive this test from the formula for the $n$ th pentatope number.

Given a positive integer $x$ , to test whether it is a pentatope number we can compute

n={\frac {{\sqrt {5+4{\sqrt {24x+1}}}}-3}{2}}.

The number $x$ is pentatope if and only if $n$ is a natural number. In that case $x$ is the $n$ th pentatope number.

Generating function

The generating function for pentatope numbers is:[4]

{\frac {x}{(1-x)^{5}}}=x+5x^{2}+15x^{3}+35x^{4}+...

Applications

In biochemistry, they represent the number of possible arrangements of n different polypeptide subunits in a tetrameric (tetrahedral) protein.

References

Deza, Elena; Deza, M. (2012), "3.1 Pentatope numbers and their multidimensional analogues", Figurate Numbers, World Scientific, p. 162, ISBN 9789814355483
Sloane, N. J. A. (ed.). "Sequence A000332". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
Rockett, Andrew M. (1981), "Sums of the inverses of binomial coefficients" (PDF), Fibonacci Quarterly, 19 (5): 433–437. Theorem 2, p. 435.
"Wolfram MathWorld site".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Deza, Elena; Deza, M. (2012), "3.1 Pentatope numbers and their multidimensional analogues", Figurate Numbers, World Scientific, p. 162, ISBN 9789814355483

[oeis-2] Sloane, N. J. A. (ed.). "Sequence A000332". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[3] Rockett, Andrew M. (1981), "Sums of the inverses of binomial coefficients" (PDF), Fibonacci Quarterly, 19 (5): 433–437. Theorem 2, p. 435.

[4] "Wolfram MathWorld site".